Back

Try This! Calculus Teaching Tips

An article detailing activities to use in your calculus classroom. Although this article does not reflect the 2019-20 updates, it remains a helpful resource. The Instructional Approaches section of the CED includes many research-based instructional strategies aligned to course skills.

This is an edited version of a lecture delivered at the AP Calculus Reading Professional Night in June 2001.

Introduction

Teaching consists of much more than standing in front of a class and spouting wisdom while our students furiously take notes (or at least appear to take notes: personally, I’m convinced that doodling is the activity that occurs most often). Thinking about what you want your students to be able to do, devising a strategy for accomplishing this, implementing your strategy, and then assessing if you even came close is what makes teaching both exciting and difficult. Students may not realize it, but our goals go far beyond having them memorize the derivative of sin x or knowing the formula for finding the volume of a solid of revolution. Producing students who are critical thinkers, self-learners, good communicators, and persistent workers is just plain hard—particularly when we are competing with the first car, the first serious girlfriend/boyfriend, the first time living away from home, the first time doing laundry! Active learning strategies are one way of getting our students’ attention and helping them become independent learners. Active learning is also one way of getting students to spend time doing mathematics—the true secret to successful learning!

My goal is to give several teaching strategies. Most of these are strategies that I’ve learned from other people and modified to use in my own classroom. I’m assuming that some of these strategies may be familiar, and that some of these ideas will be new. I certainly do not advocate using all of these techniques in one class period, or even in one year! However, I find that shaking up a class by trying something new now and then is refreshing for both my students and me. Hopefully you’ll find one or two ideas to implement, the next time you teach calculus.

In-Class Activities

Matching Games

Find some cheap stick-on nametags and make "matching pairs." Randomly pass out the nametags when students come to class and have them find their "match." For example, on one nametag write a function (written in blue) and on a second nametag write its derivative (written in red). Tell the blue tags to find their derivative and tell the red tags to find their antiderivative. This works well for doing one-step (or few-step) problems after a concept has been introduced and usually takes about five minutes.

Placemats

Create a thematic placemat (similar to those you see at restaurants with activities for kids). Include some problems, graphs, definitions, and throw in a joke just for fun. Distribute these before students get to class. Students should start working on the placemat when they come in. (Tell them it’s to keep them entertained until the “meal” is ready.) This usually takes about five minutes and works well for introducing concepts.

Multiple-Choice Questions

Write a multiple-choice question that can be done quickly. Ideally, ask a conceptual question soon after a concept is introduced. Have students choose an answer and either ask for a show of hands or have students mark their answer. Then give them one to two minutes to discuss the question with their neighbor. After the discussion, ask students to again answer the question. Typically, almost all of the class will have the correct answer after the discussion. Follow this up by making sure the students understand which answer is correct and why. This usually takes about five minutes.

For example, suppose we had talked about the relationship between a function, its first derivative, and its second derivative on the previous day. I might want to use a problem similar to AB-3 to check on their understanding of these concepts.

 

A car is traveling on a straight road with an initial velocity of 55 ft/sec. The following graph shows the car's ACCELERATION. What is happening around t = 6?

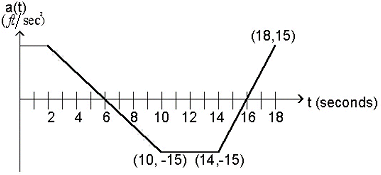
This is a piecewise-defined function shown in the first and fourth quadrants. The horizontal axis is labeled t in units, seconds, and begins at t equals zero. It is labeled every 2 units through t equals 18. The vertical axis is labeled a of t in units, feet per second squared. The vertical axis has no labeled values. The graph begins at the point 2, 15. A line is drawn from here to the point 10, -15, which is labeled. A horizontal line is drawn from the point 10, -15 to the point 14, -15, which is labeled. A line is drawn from the point 14, -15 to the point 18, 15, which is labeled.

  1. The car slows down to a stop and then continues to travel forward.
  2. The car slows down to a stop and then goes backwards.
  3. The car is going faster than 55 ft/sec and now starts to slow down.
  4. The car is going slower than 55 ft/sec.

Scripted Discussion

Write a short dialogue for students to act out in pairs. Include calculations or questions to answer as part of the dialogue. It’s helpful to use gestures as a way of monitoring where students are in the script. This works well as an introduction to a topic and usually takes 5–10 minutes.1 For the example given below, assume the students have been introduced to differential equations but you have not yet discussed symbolically solving separable equations.

 

Act out the following script with a partner, being sure to include the indicated gestures and expressions. Before starting, determine who is Alpha and who is Beta.

Alpha: Hey, Beta, I missed class yesterday. Did we do anything important?
Beta: You better not let Dr. Andersen hear you say that. She assumes we do something important every day.
Alpha: Yeah, but some days are more important that others. So what did we do?
Beta: We studied differential equations.
Alpha: So what's a differential equation?
Beta: What do you think it is?
Alpha: Uh, something with an equals sign?
Beta: (Nods head encouragingly.) That's right. What else?
Alpha: Uh, a differential?
Beta: Close. You need a derivative.
Alpha: So it's just an equation with a derivative in it. Sounds easy enough. Guess you didn't do anything important yesterday after all.
Beta: I don't know about easy. Dr. Andersen said that, in general, solving differential equations is really hard. She said that most of them can't be solved by anybody, even if they have a Ph.D. in math. So what good is getting a Ph.D. in math if you can't do hard math problems?
Alpha: Well, I don't think it sounds too hard. Here's our class outline for today. The first problem says:

Consider y' = x, y(0) = 2

  1. Why is this a differential equation?
  2. What is meant by the y(0) = 2?
  3. Solve the differential equation.

See, it can't be too bad if she expects us to solve it.
Beta: Well, the first question is easy. It's a differential equation because it has an equals sign and a derivative.
Alpha: Hey, I knew the answer to that one. What's this second question all about? It looks like math gibberish to me!
Beta: You should have been here yesterday. That's something called an initial condition.
Alpha: You just replaced symbol gibberish with word gibberish. It's still nonsense as far as I'm concerned. (Shakes head in disgust.)
Beta: Well, the solution to a differential equation is a family of functions and...
Alpha: (Interrupts Beta.) Hold it. I thought a solution was a number. You know, find a number, circle it, you're done with your math homework.
Beta: Well, differential equations are different. Your unknown is the function whose derivative satisfies the relationship in the equation. Since a derivative tells you about the shape of the curve, there isn't a unique answer. Yesterday we looked at some pretty wild graphs, called direction fields, that demonstrate this. Anyway, an initial condition gives you a point on your graph so that you have a unique solution.
Alpha: (Holds up his hand to stop Beta from saying anything else.) Hold it. That's enough. Let's go to question 3. This one looks easy. To find the function, I just need to integrate. So, I have ∫y' = ∫x. Ummm, that means that y = 1/2 x2. See, I said it was easy!
Beta: But what are you doing to do with the initial condition? You are supposed to have y(0) = 2 and for your answer y(0) = 0.
Alpha: Well, maybe the problem is just plain wrong. You said the solution to a differential equation is a family of functions. Seems to me that the solution is a single function—just like I thought it would be.
Beta: Hey, I know. (Jumps up in excitement.) You need the +c.
Alpha: (Puts head in hands and groans.) No, no, not the dreaded +c!! I always lose points for that on the exams. I thought that was just Dr. Andersen being too picky.
Beta: (Said with excitement.) No, just look. You get y = 1/2 x2. Now you can use y(0) = 2 to solve for c. So we get c = _____. (Working together, Alpha and Beta solve for c.)
Alpha: Let's see if we got it right. I think Dr. Andersen is about ready to talk about it. (Both Alpha and Beta look forward expectantly.)

Write and Critique

Put a problem on the board and give students sufficient time to work on it. When most are done, have them exchange papers with their neighbor. At this point, they are to correct the other person’s work. This works best with two- or three-step problems—something that’s not trivial but also not too difficult. This is similar to having students work problems at the board or try a problem during class with the added feature of critical reading and evaluation. It may also help some students realize the value of working together. This typically takes 5–10 minutes, depending on the problem.2

Group Writing

Put a problem on the board and tell students to begin working on it. After about one minute (before they have had time to complete the problem), tell them to switch papers with their neighbor. They must correct anything that is wrong and then keep working. After an additional one to two minutes, have them switch again. Continue having them switch periodically until the problem is complete. Students should turn in both papers with both names (each pair turns in two papers). This works best with multi-stage problems. As with Write and Critique, it emphasizes critical evaluation: students are forced to think about what they’re doing by having to finish someone else’s work. It typically takes about 10 minutes to do the problem and then discuss it.

Involuntary Discussion

Pass out index cards on the first day of class and have students write down their name and whatever other information you’d like to have. Use these cards the rest of the semester to randomly call on students to answer questions. Make sure students realize that you are not grading them on the quality of their answers. When explaining this technique, I tell students that each of them will give a brilliant answer and a stupid answer sometime during the semester. I also allow students to "pass" as long as they don’t do so continually. I typically ask 30–40 questions in a 50-minute class period so everyone is forced to become involved. This strategy gives immediate feedback as to how well the students understand the concepts, and can be used effectively for most of the class period.

For example, suppose we had finished talking about how to find local extremes and I wanted to see how well the class could "put all the information together" by going through an example similar to AB-5. My part of the discussion might go as follows:
Let p(x) = 4x3 + x2 + ax + k. We know that p(0) = 2 and that p(x) has a local maximum at x = 1. We want to find a and k.

St 1, how many pieces of information do we expect to need to answer this question? Why?
St 2, what does it mean to say that p(0) = 2? What does this mean in terms of the graph of p?
St 3, how can we use the information that p(0) = 2 to find the unknown coefficients?
St 4, do the calculation suggested by Student 3. What do you get when you substitute 0 for x? [Note: I write the steps on the board as the student dictates.]
St 5, using p(0) = 1 allowed us to find that k = 1. Can we use this same piece of information to find a? Why not?
St 6, how are we going to use the fact that p(x) has a local maximum at x = 1? What do we know about local maximums?
St 7, Student 6 suggested that local maximums give us information about the derivative. Find the derivative of p(x).
St 8, now that we found the derivative, what do we do next? Why?
St 9, Student 8 said that "a local maximum at x = 1 tells us that the first derivative of p(x) is zero when x = 1." Student 7 found the derivative of p(x). What do you get when you plug in x = 1 and set it equal to zero?
St 10, what is our answer to this problem?
St 11, what if the original question was p(x) = 4 x3 + ax2 + x + k. Could we have solved this with the same pieces of information? Why or why not?

Lecture Outlines

Write an outline for what you want to cover in class. This includes definitions, concept questions, and problems. Hand out the outline in advance and have the students use it as a means of taking notes. It guarantees that at least the problems are copied down correctly! Students can use these as a way of organizing the material. This works particularly well with the Involuntary Discussion strategy. I give students my outlines a chapter at a time. This strategy is typically used for the entire class period. Below is a sample lecture outline for a section introducing the concept of series.

Questions to be answered during class:

  1. What does it mean to say that a series is convergent?

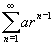
  2. Find the sum of the geometric series sum from n equals 1 to infinity of a r to the power of n minus 1 end exponent

  3. Explain why each of the following series are divergent.

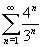
    (a) sum from n equals 1 to infinity of 4 to the power of n over 3 to the power of n

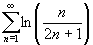
    (b) sum from n equals 1 to infinity of ln space open parentheses fraction numerator n over denominator 2 n plus 1 end fraction close parentheses

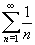
    (c) sum from n equals 1 to infinity of 1 over n

  4. Find the sum for each of the following:

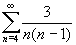
    (a) sum from n equals 4 to infinity of fraction numerator 3 over denominator n left parenthesis n minus 1 right parenthesis end fraction

    (b) 1 - 3/2 + 9/4 -27/8 + ...

  5. A certain ball has the property that each time it falls from a height h onto a hard, level surface, it rebounds to a height rh where 0 < r < 1. Suppose that the ball is dropped from an initial height of H meters.

    (a) Assuming that the ball continues to bounce indefinitely, find the total distance that it travels.

    (b) Calculate the total time that the ball travels.

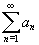  6. Suppose sum from n equals 1 to infinity of a subscript n is a convergent series (where an10). Explain why 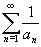sum from n equals 1 to infinity of 1 over a subscript n is divergent.

Out-of-Class Activities

Reading Quizzes

Tell the students that you truly expect them to read the textbook. Make sure they understand exactly what you want them to read and what they are supposed to understand before coming to class. For example, you could ask them to write down all of the definitions in the section, giving an example of each. Or you could ask them to give the one or two main ideas of the section plus a question they have after reading the section. I give electronic reading quizzes. The students have the questions ahead of time (as part of the lecture reading outlines) and send me the answers via email. Below is an example of the reading quiz I gave for the first section on series (the same section I used for the sample lecture outline above).

Questions to be answered before class

Please submit answers to these questions via email by 8:30 of the day the section is covered in class.

  1. What is the difference between a sequence and a series?
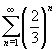
  2. Find sum from n equals 1 to infinity of open parentheses 2 over 3 close parentheses to the power of n
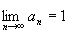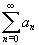  3. If limit as n rightwards arrow infinity of a subscript n equals 1, what do we know about sum from n equals 0 to infinity of a subscript n?

Electronic Discussion Board

An electronic discussion board is an effective way for students to exchange ideas about homework problems and mathematical concepts outside of class. The software that we use at Hope College is Discus (developed by a chemistry professor at Hope). The example I've attached is from a class called Mathematics for Elementary Teachers. Students were in groups of three and had to alternate doing the three assigned tasks. These were:

  • pose a problem
  • solve the problem
  • verify the solution.

This software has also been used as a means of having students ask questions on homework problems. Many professors require student to post to the board a given number of times per semester.

Grading the Exam

After giving an exam, randomly choose students’ papers and copy their answers onto another copy of the exam. The next day, give out copies of the randomly graded exam and ask students to grade it as a homework exercise. Encourage them to work together. Tell them to give each part of each problem a score of zero to three, with zero being completely wrong and three being completely right. Insist that they give comments for each problem as well as a point value. The grade for this assignment is how accurately they grade the test. Similar to the Write and Critique activity, this forces students to evaluate other people's work. This also cuts down on the time and questions you get when you hand back the exam, since students have thought about the problems after taking the test.

Early Turn-In Policy

Tell students that they have the option of turning in homework, computer labs, group problems, projects, etc. early. Typically, "early" means at least 24 hours before the assignment is due. When they turn it in, go over it quickly and make comments on another sheet of paper. These comments should be short, such as "number one is wrong," "show more work for the last part of question five," "you overlooked one case in your answer to the last part." Students have the opportunity to make these corrections before turning in the assignment for a grade. I typically have 10–25% of the class take advantage of this policy at least once. It encourages them to start their work early and is probably the only time that students actually pay attention to my comments on their papers! They learn to evaluate their work as they respond to comments. Students also appreciate having some control over the question: "What does my teacher want?" Time-wise, I think I come out even with this policy since this results in better, easier-to-grade papers.

Notes

1This activity originated from a talk by Don Cronkite; he calls his scripts "Bing and Bong."

2This activity is a slight modification of the peer review writing that is done by my colleagues in the English department.

Authored by

Janet Andersen
Hope College
Holland, Michigan