Do Cubes and Squares Have the Same Properties as Spheres and Circles?
Calculus students are often intrigued when they realize that the derivative of the volume of a sphere formula, with respect to the radius of the sphere, is the surface of the sphere formula: 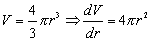 . They are also fascinated by the fact that the derivative of the area of a circle formula is the formula for its circumference:
. They are also fascinated by the fact that the derivative of the area of a circle formula is the formula for its circumference: 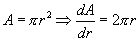 . These results don't seem to apply to cubes and squares because
. These results don't seem to apply to cubes and squares because 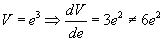 , the surface area of the cube, and
, the surface area of the cube, and 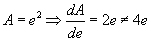 , the perimeter of the square. Why do spheres and circles behave one way and cubes and squares another?
, the perimeter of the square. Why do spheres and circles behave one way and cubes and squares another?
Consider the derivative of the area of a circle. According to the definition of the derivative:

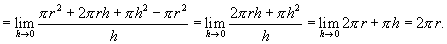
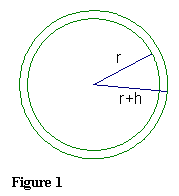
Geometrically, this result is easy to see because the region between two concentric circles, one with a radius of r and another with a radius of r + h, is essentially a band of width h and length 2πr, as shown in Figure 1.
A similar calculation is true for the derivative of the volume of a sphere. According to the definition of the derivative:
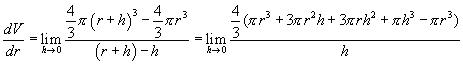
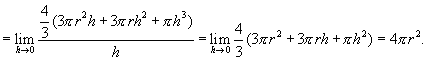
Geometrically, this result is easy to understand because the region between two concentric spheres, one with a radius of r and another with a radius of r + h, is essentially a hollow ball of thickness h and surface area 4πr 2.
Similar results don't hold for the standard formula for the volume of a cube and the area of a square, as shown in the first paragraph. Let us consider different formulas: Let s be the distance from the center of a square perpendicular to the opposite side, as shown in Figure 2. Then, since s is half the length of the edge of the square, we have the formula A = (2s)2 = 4s2, and P = 8s, for the area of a square and the perimeter of a square, respectively.
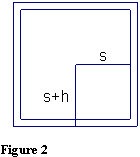
Consider the derivatives of this new formula for the area of a square. Since A = 4s2, 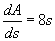 , which is our formula for the perimeter of the square. Similarly, let s be the distance from the center of a cube perpendicular to the opposite side. Then, since s is half the length of the edge of the cube, we have the formula V = (2s)3 = 8s3 for the volume of the cube, and (2s)2 = 4s2 for the area of each face. Since V = 8s3, then
, which is our formula for the perimeter of the square. Similarly, let s be the distance from the center of a cube perpendicular to the opposite side. Then, since s is half the length of the edge of the cube, we have the formula V = (2s)3 = 8s3 for the volume of the cube, and (2s)2 = 4s2 for the area of each face. Since V = 8s3, then 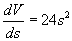 , which is 6 times the area of a face of the cube, and thus this expression is equal to the surface area of the cube. By writing the formulas in terms of s, half the length of the edge, we now have formulas that have properties consistent with those of spheres and circles.
, which is 6 times the area of a face of the cube, and thus this expression is equal to the surface area of the cube. By writing the formulas in terms of s, half the length of the edge, we now have formulas that have properties consistent with those of spheres and circles.
We can extend this result to equilateral triangles. Let e be the length of the edge of the triangle, as shown in Figure 3.
The area of the triangle is 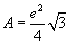 , and its perimeter is 3e. The derivative of the area is
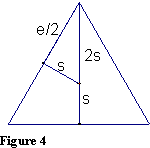
, and its perimeter is 3e. The derivative of the area is  , which doesn't remotely look like the perimeter of the triangle. Let us now change the variable and let s represent the perpendicular distance from the center of the triangle to one of the sides, as shown in Figure 4.
, which doesn't remotely look like the perimeter of the triangle. Let us now change the variable and let s represent the perpendicular distance from the center of the triangle to one of the sides, as shown in Figure 4.
Using the Pythagorean relationship, 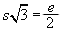 or
or 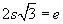 . In terms of s, the area of the triangle is
. In terms of s, the area of the triangle is 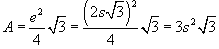 , and the perimeter is
, and the perimeter is 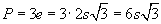 . Since
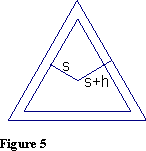
. Since 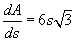 , the derivative of the area of the equilateral triangle is the perimeter of the triangle. Figure 5 shows that the difference between the triangular regions, using s and s + h, is essentially a three-sided strip of width h and length equal to the perimeter of the triangle, which geometrically confirms our result.
, the derivative of the area of the equilateral triangle is the perimeter of the triangle. Figure 5 shows that the difference between the triangular regions, using s and s + h, is essentially a three-sided strip of width h and length equal to the perimeter of the triangle, which geometrically confirms our result.
The case of the equilateral triangle suggests a way of generalizing this result to other regular polygons. The segment s, from the center of the polygon perpendicular to the side, is called the apothem of the polygon. The length of the side of the polygon then is  , where n is the number of sides, and therefore the perimeter of the polygon is
, where n is the number of sides, and therefore the perimeter of the polygon is 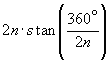 . The area of the polygon is the length of the apothem multiplied by half the length of the perimeter. In symbols:
. The area of the polygon is the length of the apothem multiplied by half the length of the perimeter. In symbols:
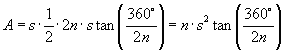
We can now check that 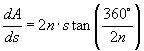 , the perimeter of the regular polygon.
, the perimeter of the regular polygon.
Challenge your students to apply this method to a regular hexagon. They should find formulas for the area and perimeter of the hexagon in terms of its apothem. They then should show that one is the derivative of the other.
We can also extend our results to three-dimensional figures. For regular polyhedra, the apothem is the radius of the inscribed sphere. Consider a tetrahedron.
The standard formulas for the volume and surface area of the tetrahedron are normally based on the length of the edge, a, of the tetrahedron. It isn't difficult, however, to rewrite them in terms of the length, r, of the apothem—the radius of the inscribed sphere.
r = radius of the inscribed sphere = apothem of the polyhedron
R = radius of the circumscribed sphere
a = length of the edge of the tetrahedron
S = surface area of the tetrahedron
V = volume of the tetrahedron

In terms of r, the inscribed radius:
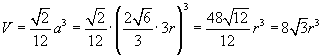

Thus, we can easily see that, in terms of the apothem, the derivative of the formula for the volume of a tetrahedron is the formula for its surface area.
Similarly, using the standard formulas for the volume and surface area of the octahedron based on the length of the edge, a, of the octahedron. We can rewrite them in terms of the length, r, of the apothem.
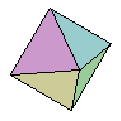
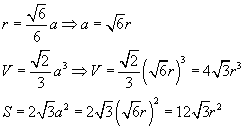
Again, it is clear that the derivative of the volume formula, with respect to r, is the formula for surface area.
Here are the formulas for the volume and surface area of the other two regular polyhedra in terms of the length of the inscribed radius, r.
Dodecahedron:
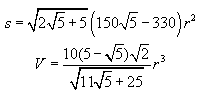
Icosahedron:
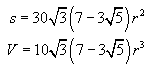
You may wish to assign students the challenging problem of verifying that the derivative of the above formula for the volume of a dodecahedron is, in fact, the given formula for its surface area.
What is the value of this result? Is it just an academic exercise? In fact, these formulas provide an easy way to find the formula for surface area of regular solids if you know the formula for its volume—or vice versa. Just write the formula in terms of the apothem of the solid and differentiate, or antidifferentiate, accordingly to find the other formula.
References
http://mathforum.org/dr.math/faq/formulas/faq.polyhedron.html#octahedron
http://mathforum.org/dr.math/faq/formulas/faq.polyhedron.html
John F. Mahoney introduced AP Statistics to Banneker High School in 2002-03 and taught 59 students that year in the course. Each of the students took the AP Exam, and Mahoney believes that they may have had the highest percentage of seniors taking AP Statistics in the country. This year he is also teaching both AB level and BC level AP Calculus. He is an AP Consultant and a longtime participant in the AP Calculus Reading. Currently, he is one of the Exam Leaders. He also chairs the editorial panel of NCTM's ON-Math: www.nctm.org/onmath. At Banneker High School, he is one of the mentors for the robotics team and helps students design gear-based drive trains—just as Banneker himself did more than 200 years ago. Many engineers help them, including those from Howard University, located across Georgia Avenue from the high school. He is one of the coaches of the school's award-winning It's Academic team. When he decided to teach at Banneker High School three years ago, after a long career in private schools, he explored Banneker's mathematics, and this paper is the result of that work.
Authored by
John F. Mahoney
Benjamin Banneker Academic High School
Washington, District of Columbia