Differentiability of Piecewise Defined Functions
Theorem 1: Suppose g is differentiable on an open interval containing x=c. If both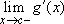 
and 
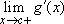exist, then the two limits are equal, and the common value is g'(c).
Proof: Let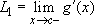 
and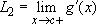 
. By the Mean Value Theorem, for every positive h sufficiently small, there exists 
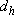satisfying 
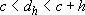such that: 
.
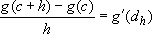Then: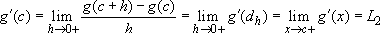 
.
Similarly, for every positive h sufficiently small, there exists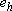 
satisfying 
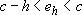such that: 
.
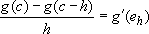Then: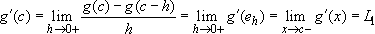 
. This shows that 
.
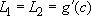Note: The same proof can be modified to show that if g is continuous at x=c and differentiable on both sides of x=c, and if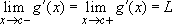 
, then g is differentiable at x=c with g'(c)=L.
Theorem 2: Suppose p and q are defined on an open interval containing x=c, and each are differentiable at x=c.
Let: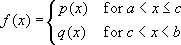 
Then f is differentiable at x=c if and only if p(c)=q(c) and p'(c)=q'(c).
Proof: We know that f'(c) exists if and only if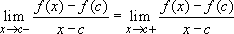 
.
We have that: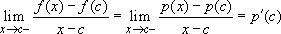 
.
Also: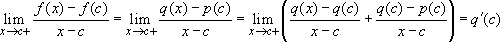 
if and only if p(c)=q(c). So f will be differentiable at x=c if and only if p(c)=q(c) and p'(c)=q'(c).
2003 AB6, part (c)
Suppose the function g is defined by: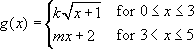 
where k and m are constants. If g is differentiable at x=3 what are the values of k and m?
Method 1:
We are told that g is differentiable at x=3, and so g is certainly differentiable on the open interval (0,5).
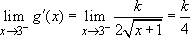and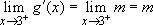 
.
So the two limits both exist and by Theorem 1 must be equal. Hence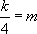 
. Since g is continuous at x=3, 2k=3m+2. This gives the two equations to solve for k and m.
Method 2:
Let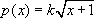 
and q(x)=mx+2. Both are differentiable at x=3. If g is differentiable at x=3, then Theorem 2 implies that p(3)=q(3) and p'(3)=q'(3). This yields the two same two equations as Method 1.
Either the note after Theorem 1 or Theorem 2 can be used to show that if we choose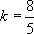 
and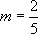 
, then we can prove that g is differentiable at x=3.
Jim Hartman teaches at the College of Wooster in Wooster, Ohio.
Larry Riddle is a professor of mathematics at Agnes Scott College in Decatur, Georgia.
Authored by
Jim Hartman
College of Wooster
Wooster, Ohio
Larry Riddle
Agnes Scott College
Decatur, Georgia