Calculus Before Newton and Leibniz

Part I

The Development of Calculus

History has a way of focusing credit for any invention or discovery on one or two individuals in one time and place. The truth is not as neat. When we give the impression that Newton and Leibniz created calculus out of whole cloth, we do our students a disservice. Newton and Leibniz were brilliant, but even they weren’t capable of inventing or discovering calculus.

The body of mathematics we know as calculus developed over many centuries in many different parts of the world, not just western Europe but also ancient Greece, the Middle East, India, China, and Japan. Newton and Leibniz drew on a vast body of knowledge about topics in both differential and integral calculus. The subject would continue to evolve and develop long after their deaths. What marks Newton and Leibniz is that they were the first to state, understand, and effectively use the Fundamental Theorem of Calculus. No two people have moved our understanding of calculus as far or as fast. But the problems that we study in calculus—areas and volumes, related rates, position/velocity/acceleration, infinite series, differential equations—had been solved before Newton or Leibniz was born.

It took some 1,250 years to move from the integral of a quadratic to that of a fourth- degree polynomial. But awareness of this struggle can be a useful reminder for us. The grand sweeping results that solve so many problems so easily (integration of a polynomial being a prime example) hide a long conceptual struggle. When we jump too fast to the magical algorithm and fail to acknowledge the effort that went into its creation, we risk dragging our students past that conceptual understanding.

This article explores the history of calculus before Newton and Leibniz: the people, problems, and places that are part of the rich story of calculus.

Finding the Volume of a Parabaloid

Abu Ali al-Hasan ibn al-Haytham (also known by the Latinized form of his name: Alhazen) was one of the great Arab mathematicians. He was born in Basra, Persia, now in southeastern Iraq. Sometime after 996, he moved to Cairo, Egypt, where he became associated with the University of Al-Azhar, founded in 970. He wrote over 90 books, and is most famous for his work in astronomy and optics. His interest in mathematics ranged over algebra, geometry, and number theory. I focus on him because he is the first person I know of to have integrated a fourth-degree polynomial.

Of course, he did not express it quite that way. Around 250 B.C., Archimedes wrote On Conoids and Spheroids, a book that, among other things, demonstrated how to find the volume of a parabaloid, the solid of revolution that you get when you rotate a parabola around its axis (see Figure 1). In particular, if a and b are positive constants and we take the region bounded above by the graph of the parabola below by the x-axis, and to the right by x = a (see Figure 2), and rotate this region around the x-axis, we get the solid of revolution whose volume is

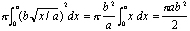
In other words, the volume is exactly half that of the cylinder that you get if you rotate the rectangle of length a and height b around the x-axis.

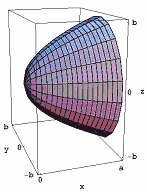
Figure 1: The parabaloid.

Figure 1: The parabaloid.

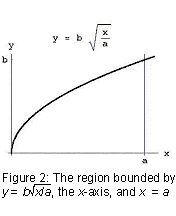
The difficult part of this calculation, something that it took a mathematician of Archimedes' stature to realize, is that the problem of finding the volume of a parabaloid can be reduced to that of finding the area under a straight line (the integral of x from 0 to a).

In the Arab world of the tenth century, Archimedes' On Conoids and Spheroids was unknown, but Thabit ibn Qurra of southern Turkey and Abu Sahl al-Kuhi of northern Iran had discovered their own proofs of the volume of a parabaloid. Ibn al-Haytham read their work and asked himself the question: What if we rotate this region around the line x = a instead of the x-axis?

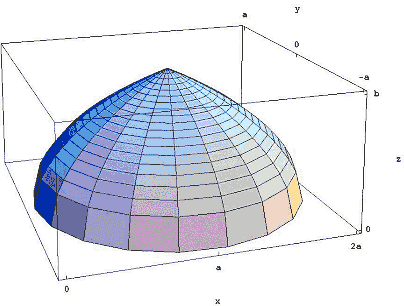
Figure 3: Rotating the region around the line x = a.

The result is the very Islamic-looking dome shown in Figure 3. Ibn al-Haytham showed that its volume is 8/15ths of the volume of the cylinder that you get when you rotate the rectangle of length a and height b around x = a. In the notation of modern calculus, the calculation of this volume becomes

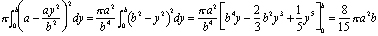
But ibn al-Haytham lived almost 700 years before the formulas for integrals would be known. He found the volume by stacking disks. If we slice the dome into nv disks, each of thickness b/n, then the ith disk from the bottom has radius a - ai²/n² and volume (b/n) p (a - ai²/n²)² (see Figure 4). The total volume of this stack of disks is

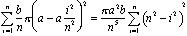
All that's left is to find a formula—in terms of n—for the summation. We then see what happens as n approaches infinity. We expand the summand and pull out the constant powers of n:

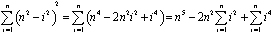
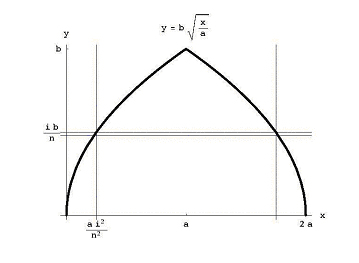
Figure 4: The horizontal slice across the dome.

For ibn al-Haytham as for mathematicians in the Middle East, South Asia, and East Asia, the problem of calculating areas and volumes came down to the problem of finding sums of powers of consecutive integers. Ibn al-Haytham was one of many mathematicians in many different places who succeeded in solving this problem. He showed that:

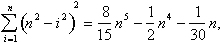
The volume of the dome is:

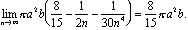
How did he find this summation? That story spans over two thousand years and three continents.

Part II

Archimedes and Sums of Squares

No description of calculus before Newton and Leibniz could be complete without an account of the contributions of Archimedes, the Greek Sicilian who was born around 287 B.C. and died in 212 B.C. during the Roman siege of Syracuse. We will look at one of the many calculus problems he studied.

It is common to credit Archimedes with the earliest stirrings of integral calculus. Among the problems he tackled and solved are finding areas under parabolas and inside spirals, and finding the volume of the sphere, spherical segments, and the parabaloid (the solid of revolution obtained by revolving a parabola around its axis). He also showed how to compute the slope of a line tangent to a spiral, the first glimmer of differential calculus.

The beauty of calculus as we now know it comes from its simplicity. The Fundamental Theorem of Calculus enables us to solve very difficult problems by applying simple calculational procedures that are justified by the Fundamental Theorem. Archimedes did not have these, so he had to rely on basic principles and, with a great deal of ingenuity, come up with clever solutions.

Archimedes found volumes of the parabaloid and other solids by using a balancing argument in which he compared the moments of different solids. He calculated the area under a parabola not by the usual method of approximating it by a sum of squares, but by using a geometric observation that enabled him to reduce the problem to finding the sum of a geometric series. This is one of a number of important uses of geometric series that contributed to the development of calculus.

The problem that I want to focus on is that of finding the area inside a spiral. In polar coordinates, the Archimedean spiral (see Figure 5) is r = kq for some constant k. In rectangular coordinates, it is the curve with parametric equations: x(t) = k · t · cos t, y(t) = k · t · sin t, t >= 0.

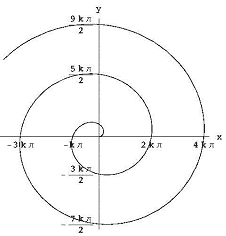
Figure 5: The Archimedean spiral

Archimedes employed what has come to be known as the "method of exhaustion." The idea is to approximate the area using ever-smaller pieces whose area can be found exactly, and then to prove that a particular value is the answer by showing that anything smaller is too small and anything larger is too large.

Archimedes attributes this method to Eudoxus of Cnidus (408–355 B.C.) who proved that the volume of any pyramid or cone is one-third the area of the base multiplied by the height. While Eudoxus found the first proof, this result is even older: it was found by Democritus (c. 465–375 B.C.). The formula for the volume of a pyramid was also discovered in ancient India, and we have record of it in the Chinese book Chiu Chang Suan Ching (Nine Chapters on the Mathematical Art) that may have been written as early as 150 B.C.

Even before anyone could prove this formula, finding it required thinking of the pyramid as made up of thin slices, three sets of which could be reconfigured to make a rectangular block. Later in this article we'll see how this mental three-dimensional geometry led Archimedes to the formula he needed to find the area of the spiral.

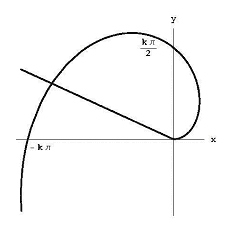
Figure 6: The area bounded by the Archimedean spiral and the ray q = q₁.

Approximating the Area of the Spiral

To find the area bounded by the spiral and the ray q = q₁, as shown in Figure 6, we divide the angle between the rays into n small angles of size q₁ / n. If we look at the ith piece of angle, the spiral's distance from the origin increases from k(i - 1) q₁/ n to ki q₁/ n. This means that our area lies inside the sector of radius ki q ₁/ n. Our area entirely includes the sector of the circle of radius k(i - 1) q₁/ n.

The angle q₁/ n represents q₁ / 2 p n of a full circle, so the area of this sector is somewhere between

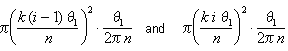
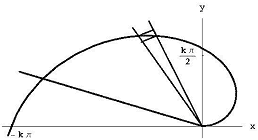
Figure 7: The sector between q = k(i - 1)q₁/n and q=ki q₁/n

When we simplify these bounds, we see that the area of the ith segment lies between k²q ₁³ (i - 1)²/2n³ and k²q₁³ i² /2n³. The total area lies between

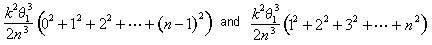
At this point, Archimedes derived a succinct formula for the sum of the first n - 1 squares:

.

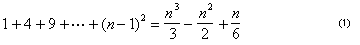The area under the spiral lies somewhere between

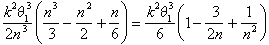
and

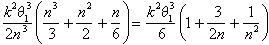
As Archimedes now argued, the only number that lies between these bounds for all values of n is k² q₁³ /6.

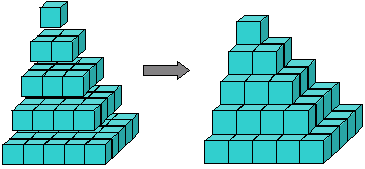
Figure 8: The pyramid of squares

The Formula for the Sum of Squares

The formula for the sum of squares may not have been new to Archimedes, and there is evidence that it might have been discovered about the same time in India. We do know that it was rediscovered many times. The earliest proofs, including Archimedes's proof, are all geometric.

We can visualize the sum of squares as a pyramid built from cubes (Figure 8). Archimedes showed how to take three of these pyramids together with a triangular layer of blocks representing 1+2···+(n - 1) and fit them together to get a block of cubes n x n x (n - 1). In other words, he showed that

.

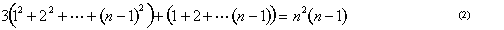The formula 1+2+···+(n - 1)=n (n - 1)/2 is often attributed to Gauss. The story is that he discovered it when his teacher ordered him to add the integers from 1 through 100. In fact, it is an ancient formula. It can be found, for example, in India in a Jain manuscript from 300 B.C.: it would have been part of Archimedes's own mathematical instruction. It has a very simple geometric proof as shown in Figure 9.

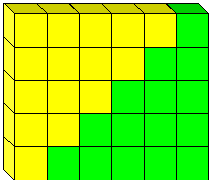
Figure 9: The proof that 2[1+2+···+ (n-1)] = n(n-1)

We still have to prove equation (2), but once we know it is true, we can combine it with the formula for the sum of the first n - 1 integers to get

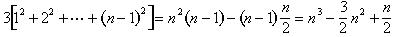
Divide both sides by 3, and we get equation (1).

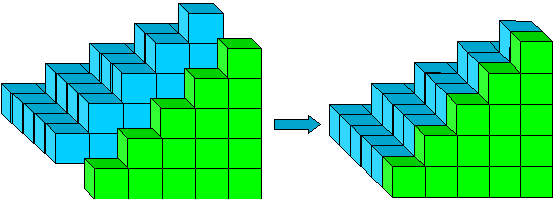
Figure 10: 1²+2²+···+(n - 1)² +1+2+···+(n - 1).

The tricky part of proving equation (2) is to see what you get when you combine a pyramid, 1² + 2² + ··· + (n - 1)² , and the triangular array 1+2+ ··· + (n - 1). This is shown in Figure 10, which can be thought of as a pyramid of rectangles: 1·2+2·3+ ··· + (n-1)². We split this rectangular pyramid into two pieces (Figure 11).

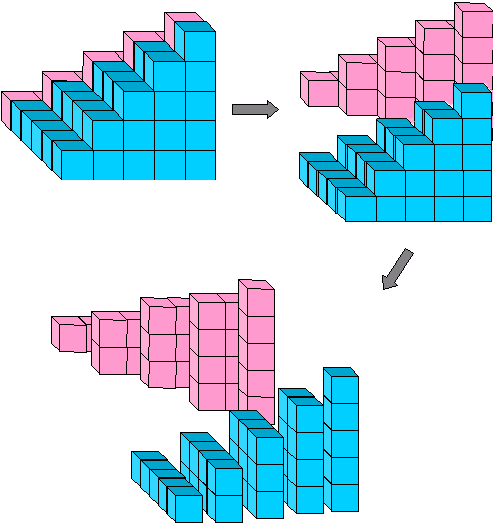
Figure 11: 1· 2 + 2·3 + 3·4 +···+ (n-1)n = 2[1(n-1)+2(n-2)+3(n-3)+ ···+(n-1)1]

The algebraic equation that corresponds to this picture is

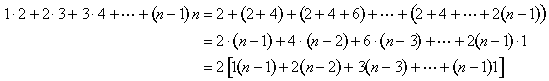
These pieces fit around the green pyramid in Figure 8 so that one more inverted pyramid completes the n x n x (n - 1) block (Figure 12):

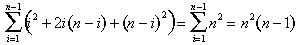
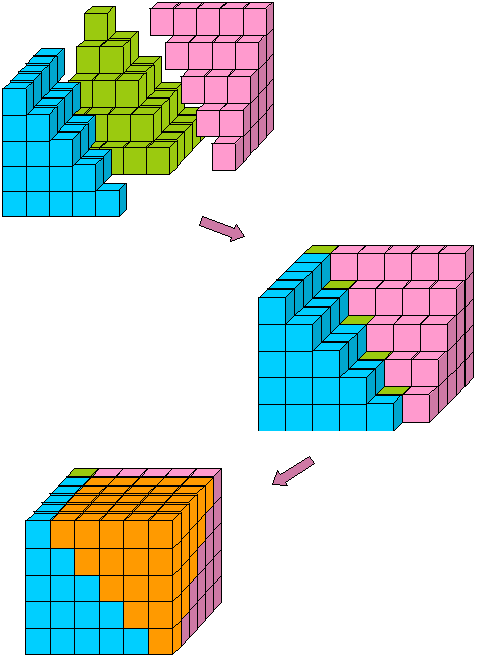
Figure 12: The n x n x (n - 1) block assembled from three sums of squares and one sum of integers.

Sums of Cubes

You might think that having seen how useful the sum of squares formula is, Archimedes would then have found the formula for the sum of cubes. He didn't. It took over a thousand years before anyone did. The problem is that sums of squares are easy to see geometrically. Sums of cubes can be visualized, but the object you want to put them together to form is four-dimensional. But as we'll see in Part III, by the time Europe was in its Middle Ages mathematicians in the Middle East, India, and China had all done so.

Part III

Sums of Powers

In the first two parts of this article, we saw how Archimedes and ibn al-Haytham used formulas for sums of powers to evaluate areas and volumes. Starting in the 11th century, Arab, Chinese, and Indian mathematicians began to discover techniques that would enable them to find the area under any polynomial. But before anyone could discover such formulas, they had to invent polynomials. Quadratic and cubic polynomials had existed for well over a thousand years, but expressed as areas and volumes. It was not even clear what a fourth power would mean. Higher-degree polynomials emerged almost simultaneously around the year 1000 in the Middle East, India, and China.

Two 11th-century contemporaries, Abu Bakr al-Karaji in Baghdad and Jia Xian (a Chinese court eunuch) studied polynomials of high degree, found methods for extracting roots, and discovered what we today call Pascal's triangle. Al-Karaji gave the first known proof of the formula for the sum of cubes—also one of the earliest known examples of a complete proof by induction.

Sums of Cubes

When you sum cubes of successive integers, you quickly find a pattern:

1³ = 1, 1³ + 2 ³ = 9, 1³ + 2³ + 3³ = 36, 1³ + 2³ + 3³ +4³ = 100, 1³ +··· +5³ = 225.

These are all perfect squares, and not just any perfect squares, but

1², 3² = (1 + 2)², 6² = (1 + 2 + 3)², 10² = (1 + 2 + 3 + 4)², 15² = (1 + ··· + 5)².

The formula for the sum of cubes is easy to guess:

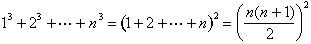
Aryabhata of Patna (in what is now India) discovered this formula around 500 C.E., and it may have been known even earlier. It would be rediscovered by Abu al-Saqr Abd al-Aziz ibn Uthman al-Qabisi in 10th-century Baghdad and again in early 14th-century France by Levi ben Gerson. Nilakantha of Kerala (in southwest India) gave a visual proof in 1500 that captures the essence of al-Karaji’s proof.

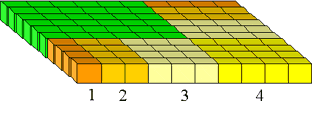
Figure 13: The (1 + 2 + ··· + n)X(1 + 2+ ··· + n) square.

Begin with the square (1 + 2 + ··· + n)² (Figure 13). We take out the smaller (green) square of size (1 + 2 + ··· + (n - 1))² and are left with the blocks shown in Figure 14, which can be rearranged into a cube.

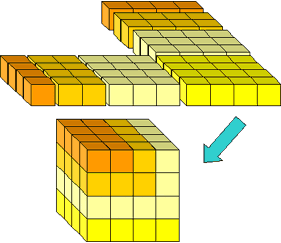
Figure 14: Rearranging the remaining blocks into a cube.

This provides the inductive step for the proof:

(1 + 2 + ··· + n)² = n³ + (1 + 2 +··· + (n - 1))².

Sums of Fourth Powers

In Part I of this article, we saw that ibn al-Haytham needed sums of fourth powers to find the volume of the solid obtained by rotating a parabola around a line perpendicular to the axis of symmetry. He found such a formula. While we have no evidence that he pushed his technique beyond fourth powers, his approach can be used to find formulas for sums of consecutive integers to any power.

Al-Haytham began with the formula for the sum of cubes. He used it to bootstrap up to a formula for sums of fourth powers. This begins with the observation that k + 1 can be written as a sum of k + 1 1s or as 2 plus a sum of k - 1 1s or as 3 plus a sum of k - 2 1s, and so on:

(1³ + 2³ + ··· + (k - 1) ³ + k³ )(k + 1)

= 1³(1 + 1 + ··· + 1) + 2³ (2 +1 +··· + 1) + ··· + (k -1)³ ((k - 1) + 1 + 1 ) + k³(k + 1)

= (1⁴ + 1³ + ··· + 1³) + (2⁴ + 2³ + ··· + 2³) + ··· + ((k - 1)⁴ + (k - 1)³ + (k - 1)³ ) + (k⁴ + k³)

We reorder the last sum, putting the fourth powers together and regrouping so that we get sums of consecutive cubes:

(1³ + 2³ + ··· + (k - 1)³ + k³ )(k + 1)

= (1⁴ + 2⁴ + ··· + (k - 1)⁴) + k⁴ ) + 1³ + (1³ + 2³) + (1³ + 2³ + 3³) + ···

+ (1³ + 2³ + ··· + (k - 1)³ ) + (1³ + 2³ + ··· + k³)

We now use the formula for the sum of cubes:

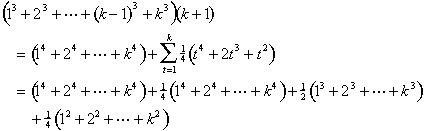
We consolidate similar terms and use the formulas for the sums of cubes and squares once more:

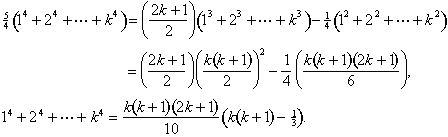
The same idea will work to find a formula for the sum of fifth powers in terms of the sum of fourth powers, and so on.

Higher powers

In 12th-century Baghdad and then independently in 14th-century India and China, mathematicians discovered and exploited a remarkable property of Pascal’s triangle. Starting at the edge, come down any diagonal that heads southwest, adding the entries. Wherever you stop, the sum of these numbers is the next number to the southeast:

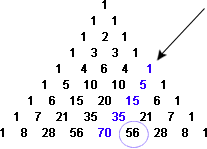
Figure 15: The sum of terms on a southwest diagonal (1+5+15+35) equals the next term to the southeast (56).

We can express this in terms of polynomials. We define a polynomial of degree n:

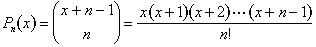
This property of diagonal sums implies that for positive integers n and k, we always have

P_n(1) + P_n(2) + ··· + P_n(k) = P_{n + 1}(k).

We can use this to find sums of arbitrary powers because any polynomial of degree n, including xⁿ, can be expressed in terms of P₁(x), P₂(x, ... , P_n(x)). For example,

x⁴ = 24P₄(x) - 36P₃(x) + 14P₂ (x) - P₁(x).

It follows that

1⁴ + 2⁴ + ··· + k⁴ = 24P₅(k) - 36P₄(k) + 14P₃(k) - P₂(k).

This fundamental relationship for binomial coefficients first appeared in Al-Bahir fi'l Hisab (Shining Treatise on Calculation) written by al-Samaw'al in 1144 in present-day Iraq. It also can be found in Siyuan Yujian written by Zhu Shijie in 1303 in China, and the Ganita Kaumudi written by Narayana Pandita in 1356 in India.

Remarkable as this method is, it is not the best way of finding formulas for the sums of powers. That was discovered by the Swiss mathematician Jacob Bernoulli at the beginning of the 18th century. For two thousand years, mathematicians had been using sums of powers formulas in order to calculate areas. Bernoulli used integral calculus to find simple derivations of the sum of powers formulas. But that is another story.

Resources

Calinger, Ronald. A Contextual History of Mathematics: To Euler. Upper Saddle River, N.J.: Prentice Hall, 1999.

Dick, Thomas P., and Charles M. Patton. Calculus. Boston, Mass.: PWS Publishing, 1995.

Dijksterhuis, E. J. Archimedes. Translated by C. Dikshoorn. 1938. Princeton, N.J.: Princeton University Press, 1987.

Heath, Thomas. A History of Greek Mathematics. 2 vols. Oxford: Oxford University Press, 1921. Reprint: Dover, 1981.

Katz, Victor J. A History of Mathematics: An Introduction. 2nd edition. New York: Harper Collins, 1998.

———. "Ideas of Calculus in Islam and India." Mathematics Magazine 68-3 (1995): 163–174.

Martzloff, Jean-Claude. A History of Chinese Mathematics. Translated by Stephen S. Wilson. New York: Springer-Verlag, 1998.

Saraswathi, T. A. "The Development of Mathematical Series in India After Bhaskara II." Bulletin of the National Institute of Sciences 21 (1963): 320–343.

Stein, Sherman. Archimedes: What Did He Do Besides Cry Eureka? Washington, D.C.: The Mathematical Association of America, 1999.

Authored by

David Bressoud
AP Calculus, Macalester College
St. Paul, Minnesota