Graphing Calculator Simulations Simplified
Univariate Data Sets
Obviously, for students to best experience a simulation, they should actually conduct the activity—for example, flip a coin 500 times or roll the die 600 times, etc. I do in fact have my students participate in simulation activities in order to see and experience the results firsthand. There are times, however, when a quick run on the calculator can produce results for either demonstration purposes in class by the teacher or by students for easy data collection.
Think about the time in class that you discuss uniform distribution, and you ask your students for examples of data that would produce a uniform distribution. Many will tell you that rolling a die would. You can quickly run a simulation and graph the results for your students.

Press MATH and arrow over to PRB, select 5:randInt(.
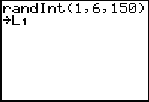
Type 1, 6, 150. These are the start and stop boundaries and 150 rolls of the die, then STO into L1.
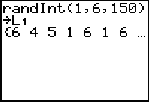
The list is also displayed on the home screen.
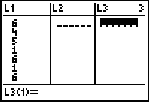
Press STAT-1: edit to view the list.
An easy way to view the distribution is to draw a histogram. Students will have to manually set the window values in order for the discrete values of 1 through 6 to be shown.
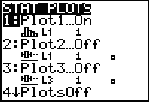
Press 2nd-STATPLOT, choose 1:.
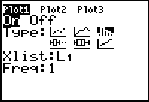
Highlight the histogram, and the X-List is L1.
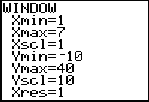
The window is shown above. The reason the x-max is 7 is because you must show the right-hand bar boundary.
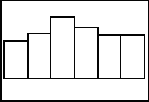
Press GRAPH, and the histogram is shown.
You will notice that the graph does not look quite uniform. This is the beauty of the calculator simulation. Another simulation can be run immediately and another display shown as well. Students can explore the idea of increasing the number of die rolls to see if that changes the shape of the distribution.
There are a couple of ways to show the count of each roll. One way is to TRACE along each bar of the display.
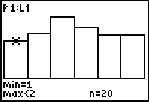
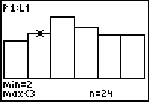
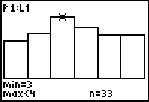
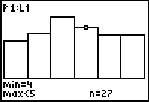
Since the values of the histogram are discrete, min = 1 and max
Students can also arrange the list items in ascending or descending order and then manually count how many of each roll there are.
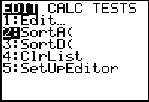
Press STAT-2: SortA and ENTER.

Choose the list you want to sort.

Press ENTER.
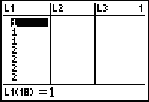
View the list and see that the items are in ascending order. The students can count how many of each number if they wish.
If you are discussing with students what happens in the long run, students can keep a tally of how many of each roll came up for many simulations. Sums and averages of the values can be taken, and a discussion can take place. Below are four more histograms with different sample sizes of the die rolls.
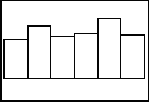
n = 150
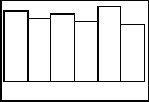
n = 250
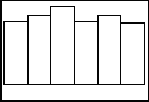
n = 350
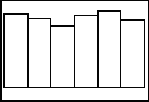
n = 500
If students are in groups and they each run these simulations, displays can be compared. This gives students even more simulations to analyze. Besides just looking at the frequency of each die roll, means, medians, and other measures can be taken using the calculator. Why not have the students come up with the questions that you want answered?
Design
As the course progresses, students will need to set up simulations in design problems. The random digit table is used often to conduct these simulations, especially in an assessment situation. We can use an example (hypothetical data) where it has been shown that 40 percent of all students in the state of Illinois will go to college out of the state. If you take a random sample of 300 students, how many would be going to colleges out of state according to your simulation? Students will get a variety of solutions, but in the long run what will happen? First we set up the assignment of the digits. We can use single or double digits to represent the in-state and out-of-state students. Let's keep it simple and use 0, 1, 2, and 3 to represent the 40 percent of the students going out of state and 4, 5, 6, 7, 8, and 9 to represent the in-state students. Run a simulation of 300 students as follows:
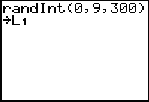
Press Math-PRB-5:randInt, type in the values above, STO into L1.
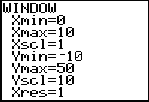
Change the viewing window so it's appropriate for the display.
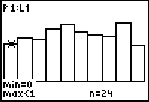
TRACE along and add up the counts for the first four bars.
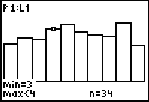
The sum will be the number of students going out of state in your simulation.
In the above simulation, there were 113/300. This corresponds to approximately 37.6 percent, close to the expected 40 percent. (Of course, this is just one simulation.) The random digit table can be used for the same simulation but would take a bit longer.
Random Table Line Numbers
When I have students in a group activity using the random digit table, I want them to begin on different line numbers so we have different sample values. This can also be accomplished on the calculator by seeding the initial draw. I have students use the last four digits of their phone numbers as their seed value, so essentially they are starting on a different line than the next student. You are not limited to four digits; you can store with less or more if you like.

Type in the number to seed and press STO.

Press MATH-PRB-1:rand.

Press ENTER; it displays on the home screen.
Press ENTER again, and the calculator is seeded.
Robin Levine-Wissing has taught mathematics for 26 years and has served as an AP Reader for 5 years. She has been a T3 (Teachers Teaching with Technology) national instructor for 10 years and a College Board consultant for 5 years. Robin was a co-author of an article entitled "Computer Physics on the Playground" in The Physics Teacher in 1995. Robin has presented over 100 workshops and institutes all over the United States and Canada. She currently teaches AP Statistics and precalculus in Naperville, Illinois.
Authored by
Robin Levine-Wissing
Naperville North High School
Naperville, Illinois