Coke® Versus Pepsi®: An Introductory Activity for Test of Significance
Part I: Setting the Stage
The following activity is a great way to “set the stage” on the first day of class and give your students an overview of what they’ll be studying during the year. It involves a simulation, a graphical representation, experimental design, data collection, and hypothesis testing, and it can easily be done in the space of 90 minutes, or 45 minutes if you provide data that were already collected.
You will need:
- About a hundred 3-ounce Dixie cups
- About three liters of Coke and three liters of Pepsi (less for a smaller class)
- Unsalted crackers for students to “cleanse the palate”
- Standard dice: 256 for a class of 32 students working in groups of four, and more for either larger classes or for students working individually. Dice in large quantities can be purchased from school supply houses, and they are such an asset to a statistics class that the purchase of a very large classroom set is well worth the investment. It is also possible to do the activity with fewer dice – one die per student or group – and have each student or group roll a single die repeatedly instead of rolling many dice at once.
The question of interest:
“Can anyone in this class tell the difference between Coke and Pepsi by taste?”
Many students will say that they can. The activity is designed to find out. The activity will have two parts to it: a “tasting part” in which data are collected outside of the classroom in the hall, and a “simulation part” in which students in the classroom conduct a simulation with dice.
Two student volunteers proceed out to the hall and make the following preparations. First, they will label three cup positions “A,” “B,” and “C.” Then they will roll a die and pour drinks into the cups according to the following plan:
Figure 1:
| Die Roll | Cup A | Cup B | Cup C |
|---|---|---|---|
| 1 | Coke | Pepsi | Pepsi |
| 2 | Pepsi | Coke | Pepsi |
| 3 | Pepsi | Pepsi | Coke |
| 4 | Pepsi | Coke | Coke |
| 5 | Coke | Pepsi | Coke |
| 6 | Coke | Coke | Pepsi |
As you can see, all combinations of two of one drink and one of the other are represented, and the die roll makes each combination equally likely.
While one student pours the drinks, the other keeps track of the treatment – that is, which cup contains the different drink. It might be helpful for the students if you already have prepared a data sheet with column headings of “Subject number,” “Treatment,” and “Response.” The first few entries by the students might look like this:
Figure 2:
| Subject number | Treatment | Response |
|---|---|---|
| 1 | 2 (PCP) | B |
| 2 | 6 (CCP) | C |
| 3 | 3 (PPC) | C |
Students will be called out into the hall one by one to taste the three drinks and decide which cup contains the different drink. They do not need to identify the drinks as Coke or Pepsi, they only have to identify the cup containing the different soda, either A, B, or C.
They return to the classroom and write their choice on the board in a table that is similar to the one the students have in the hall. The table in the classroom leaves the Treatment column blank, while the other leaves the Response column blank. The table on the classroom blackboard might begin like this:
Figure 3:
| Subject number | Treatment | Response |
|---|---|---|
| 1 | B | |
| 2 | A | |
| 3 | C |
While this is going on, students in the classroom can do the simulation activity, which begins with the question, “Suppose that in fact no one could tell the difference between Coke and Pepsi. How many people do you think would identify the correct cup anyway?”
A few students may think at first that there is a 50 percent chance of guessing correctly by chance, but in fact the chance is one-third, since there are three cups. So if the class has 30 students, you’d expect about 10 of them to guess right just by chance.
Next question: “Exactly 10? Do you think 11 might guess right just by chance? Or 12? Or 9?”
You should help students see that if everyone is just guessing randomly, then although you might get exactly one-third of the class guessing correctly, you might also reasonably get a few more than 10 or a few fewer than 10 correct identifications. “How about 15?” you might then ask. “Could we get 15 correct responses? 25?”
As you increase the number, students should respond that yes, it is possible to get 25 correct responses out of 30 random guesses, but it isn’t very likely. Getting as many as 25 correct responses out of 30 random guesses would be considered a very unusual fluke.
Ask “So if 25 out of 30 named the correct cup, what would you conclude?” Guide the students to a conclusion that “at least some people in the class can really tell the difference between Coke and Pepsi and are not just guessing.” Some may say that the 25 who got it right could tell the difference and the other five could not, but that’s not necessarily true. Some of the 25 might have just given lucky guesses.
Estimating just how many people can actually tell the difference is beyond the scope of this activity, and indeed would be a somewhat tricky question for students even after completing the AP Statistics curriculum. Rather, the conclusion students should draw from “25 out of 30 correct cup identifications” is that at least some people in the class can tell the difference.
Part II: Using a Histogram
The next stage of the discussion (students should still be discreetly filing in and out of the classroom to taste the drinks) is to ask the students how many correct identifications they need before they can conclude that people were not just randomly guessing: “11 out of 30 is more than a third, but not enough more to be convincing, right?”
That’s what you said earlier. Now ask “Is 25 out of 30 convincing? Yes? What about 20? What about 15? How many would we need to see before we’d be convinced that some people were not just randomly guessing?”
Students will probably volunteer different dividing lines, but they will not be good at defending them. At the point when all the students understand the question but are unsure of how to answer it, the dice should be introduced into the activity.
If you have enough dice, then each student or student team should receive as many dice as there are students in the class who are participating in the study as subjects. If there are not enough dice, then each student or student team should receive one die and be instructed to roll it as many times as there are subjects in the study.
Ask “Suppose we let each die rolled represent a person participating in this study. If no one can tell the difference between Coke and Pepsi, then what is each person’s chance of naming the correct cup anyway, by sheer luck?” It’s one-third.
Then ask “What can we do with the dice that will simulate our whole class all just guessing blindly?” You would like for the students themselves to suggest a simulation in which two die outcomes (say, 1 and 2) are considered a correct cup identification, and the other four die outcomes (say, 3, 4, 5, and 6) are considered incorrect cup identifications. If no one can really tell the difference, then the whole class will behave essentially like a collection of rolled dice, with 1s and 2s representing correct cup identifications.
It is helpful to have on the board a number line drawn near the chalk tray, with marks at every integer from zero up to the number of students participating in the study. On this number line, you will build a histogram of Xs.
At this point, demonstrate by rolling a set of dice yourself (or one die many times). You should have as many die rolls as there are subjects in the study. Count the 1s and 2s. Suppose there are 8 out of 30 that “guessed correctly.” On your number line at the blackboard, make an X over the number 8. Ask your students or groups to do five or 10 simulations each (it’s good to have about 100—200 simulations) and then come to the blackboard and stack their Xs over the appropriate integers, making a histogram of the distribution of “number of correct cup identifications if everyone is randomly guessing.”
Figure 4 shows one possible result, based on 100 simulations of 30 subjects (die rolls) randomly guessing.
Figure 4:
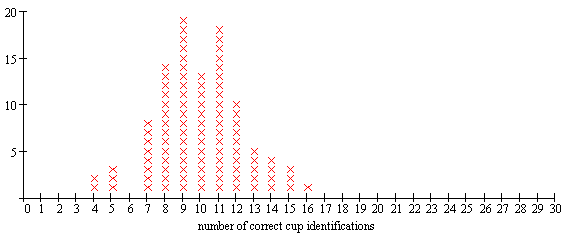
Ideally, the tasting and simulation parts would conclude at the same time. If the simulation part concludes first, then students may simply do more simulations or something else to fill class time. You can’t stop the tasting prematurely – once you’ve begun the simulation, you’ve committed to that many subjects in the experiment, and they now must finish!
Upon conclusion of the tasting, the student volunteers in the hall return to the classroom and complete the data table on the blackboard, writing the treatments (only the letter of the different soda is necessary) next to the response for each subject. The number of correct identifications is then counted.
At this point, if the number is unusually high (say, 18 out of 30), then most students are prepared to conclude (correctly) that there is evidence that at least some people can tell the difference between Coke and Pepsi.
It is probably worth the effort to get them to explain their reasoning clearly. Some statement like this would be great: “If everyone were randomly guessing, we would almost never see 18 students get it right by luck, because we did that 100 times with dice, and the highest we ever got was 16, and that was only once.”
In my experience, usually about half or a little more will identify the correct drink. If the number who identify the correct drink is sufficiently close to one-third of the class, this would be interpreted as no clear evidence that people were not just randomly guessing, and students should draw that conclusion.
Note that the conclusion is not that no one could tell the difference between the drinks, only that we have no evidence that anyone could.
Note also that no conclusions can be drawn for people in general unless we make the assumption that this class is “representative” of “people in general” in their Coke/Pepsi distinguishing ability. This is a dubious assumption; for one thing, the students are all about the same age, and age may have an effect on someone’s ability to tell the difference. Students may identify other things they have in common that may make them “unrepresentative” of the population at large.
If you have a short class period or would like to do the simulation activity without the actual collection of data, you may want to use data that I collected when I did this activity with my class: 13 out of 21 students correctly identified the different drink.
This activity is also good for introducing tests of significance later in the school year. It is clear, however, that nothing in it is beyond students on their first day of class, yet it sets the stage for much of what is to come. Good luck!
Authored by
Floyd Bullard
North Carolina School of Science and Mathematics
Durham, North Carolina