Beginning the Year with Local Linearity
After beginning the last seven or eight years of both AB and BC Calculus classes with an exploration of local linearity, I am delighted with how well the students respond and with the level of understanding of the concept of derivative that they develop in this unit. It is never the same—from year to year and from class to class—and I continue to refine the unit as new questions from students prompt new insights into how to make the conceptual components even more accessible. So it keeps me fresh and excited about teaching as well.
In this article, I have included a brief overview that I share with teachers in my summer institutes. I often spend two or three weeks in exploration mode and in having student questions and comments direct "next steps" (which is why the unit is not preprogrammed and thus transferable to the printed page). In recent years, it is often well into week three (of 45-minute classes) before we actually get to developing formal derivative rules or take on concepts/applications related to the derivative. However, in those first weeks, the discussions are rich and much is learned. Note that I do not introduce a formal definition of limit until close to the end of this unit, and I only do so to be sure that students get a glimpse of how the definition "tightens up" the "closeness" issue.
In addition, I have tried to outline for you other specific activities (in the section "Next Steps in Local Linearity") that I pick and choose from as the exploration continues.
Local Linearity: A Brief Overview
The Derivative
Technology to the Rescue:
Next Steps in Local Linearity
Local Linearity: A Brief Overview
A function f is said to be linear over an interval if the difference quotient:
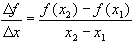
is constant over that interval. Although few functions (other than linear functions) are linear over an interval, all functions that are differentiable at some point where x = c are well modeled by a unique tangent line in a neighborhood of c and are thus considered locally linear. Local linearity is an extremely powerful and fertile concept.
Most students feel comfortable finding or identifying the slope of a linear function. Most students understand that a linear function has a constant slope. Our goal should be to build on this knowledge and to help students understand that most of the functions they will encounter are "nearly linear" over very small intervals; that is, most functions are locally linear. Thus, when we "zoom in" on a point on the graph of a function, we are very likely to "see" what appears to be a straight line. Even more important, we want students to understand the powerful implications of this fact!
The Derivative
If shown the following graph and asked to write the rule, most students will write f(x) = x. This shows some good understanding, but not enough skepticism.
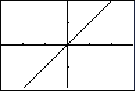
If the viewing window [-.29,.29] x [-.19,.19] were known, some students might actually question whether enough is known to conjecture about the function presented.
In the viewing window [-4,4] x [-2,2], a very different graph is observed:
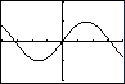
As teachers, we understand that the first window gets at the idea of local linearity (in the neighborhood of x = 0) of the differentiable function we see in the second window. In fact, the two windows are also supportive of an important limit result:
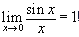
Our ultimate goal, however, is to have students come upon at least an intuitive understanding of the formal definition of the derivative of a function f for themselves. They should be able to say, "Of course!" rather than question, "What is that?" when presented with that formal definition. It is technology that makes this approach possible, and that helps students understand the concept of derivative rather than merely memorizing some obscure (to them) notation.
Technology to the Rescue:
Discovering Local Linearity of Common Functions
Start with a simple nonlinear function, say 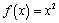 . Select an integer x-value and have students "zoom in" on that point on the graph until they "see" a line in their viewing window. Ask them to use some method to estimate the slope of the "line" and be ready to describe their process. Most will pick two nearby points and use the slope formula. If they have done as instructed, they should all be finding a slope value very nearly the same. If not, ask them to work in small groups until everyone has agreed on some common, reasonable estimate. This will allow them to check their method and become comfortable with the technology.
. Select an integer x-value and have students "zoom in" on that point on the graph until they "see" a line in their viewing window. Ask them to use some method to estimate the slope of the "line" and be ready to describe their process. Most will pick two nearby points and use the slope formula. If they have done as instructed, they should all be finding a slope value very nearly the same. If not, ask them to work in small groups until everyone has agreed on some common, reasonable estimate. This will allow them to check their method and become comfortable with the technology.
Next, assign pairs of students their own, personal x-coordinate. In fact, if the class is small, you might assign two or more x-coordinates to each pair. Be sure to assign both positive and negative x-coordinates within an interval, say [-4,4]. Most of the assigned values will be given in tenths. Make a table of results (either on the board or using the statistics capabilities of your overhead calculator). The class should discover on their own that there appears to be a predictable relationship between the x-coordinate and the resulting slope. In fact, they are likely to make a conjecture about the general derivative function without even realizing what they are doing.
This conjecture can be confirmed using the difference quotient and an intuitive idea of limit as follows: If a student group was assigned the x-value of a, then they would have predicted the slope of a line containing the point (a,a2). When they zoomed in, a nearby coordinate might have been (x, x2). Thus, their predicted slope would have been 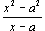 , which can be easily simplified t
, which can be easily simplified t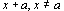 . If x is "very close" to a in value, then the predicted slope should have been almost 2a!
. If x is "very close" to a in value, then the predicted slope should have been almost 2a!
Next Steps in Local Linearity
Other days are spent on the following activities. I have tried to put them in a logical order, but I really do let the student questions and comments dictate which of these I use and in what order. Some of these explorations make wonderful homework assignments, by the way. When I use them as such, students gather the data and make conjectures, but class discussion always follows to uncover what students are beginning to understand and how they are understanding the concepts.
- Explore other simple power functions as we did
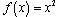 . This is often done as portions of homework assignments. I will often introduce another notation, specifically leading to
. This is often done as portions of homework assignments. I will often introduce another notation, specifically leading to 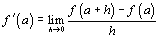 , and have students confirm conjectures using this notation as well. Thus we review factoring polynomials of the form xn - an and expanding binomial powers of the form (x + a)n in context. Almost always, students will want to know if the pattern they observe will always hold, and thus (to answer that question) we actually prove the Power Rule for positive integers.
, and have students confirm conjectures using this notation as well. Thus we review factoring polynomials of the form xn - an and expanding binomial powers of the form (x + a)n in context. Almost always, students will want to know if the pattern they observe will always hold, and thus (to answer that question) we actually prove the Power Rule for positive integers. - Explore
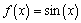 .
.
This is often done as a class project. I assign each student a decimal value and have them zoom in on the curve at the x-value. They are to find the slope of a good linear model for the graph by using the "zooming in until you think you are viewing a linear function" approach. Then we collect the data and plot the results. I do not try to confirm their conjectures with a formal proof at this point, but they are firmly convinced that Dx(sin x) = cos xat this stage! If the mood seems right, I often lay the groundwork for the Chain Rule by asking them to follow this activity up with one that explores the functions
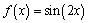 and
and 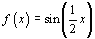 . We get to think about why there appear to be factors of
. We get to think about why there appear to be factors of
2 and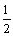 , respectively.
, respectively. - Have students enter the function
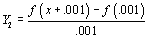 in their (TI-83) calculators and explore other functions. Of course, I check to make sure they understand that this allows the calculator to easily do exactly what we have been very tediously doing—and we get a whole screenful of results. We often begin by verifying that this yields the same "pictures" that we had been painstakingly getting by plotting individual student data with functions already explored above. However, I often begin to insert functions involving other simple transformations, such as
in their (TI-83) calculators and explore other functions. Of course, I check to make sure they understand that this allows the calculator to easily do exactly what we have been very tediously doing—and we get a whole screenful of results. We often begin by verifying that this yields the same "pictures" that we had been painstakingly getting by plotting individual student data with functions already explored above. However, I often begin to insert functions involving other simple transformations, such as 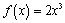 ,
, 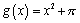 , and
, and 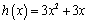 . Students quickly recognize many of the patterns that such variations generate, and they do a lot of algebra review in the process of confirming their conjectures—not to mention developing other derivative rules rather painlessly and within context.
. Students quickly recognize many of the patterns that such variations generate, and they do a lot of algebra review in the process of confirming their conjectures—not to mention developing other derivative rules rather painlessly and within context. - Explore
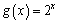 . This function is much harder for students to deal with than previous functions, but most students, using the approach above, "guess" that the SlopeFinding function (a.k.a. the derivative) is exponential. Some will even hone in on the constant factor that appears to be the stretch factor involved. There is a wonderful exploration that leads students to discover, with very little help from the teacher, that Dx(bx) = b x 1nb. It's a little too long to include here, but ask questions if you want to know more.
. This function is much harder for students to deal with than previous functions, but most students, using the approach above, "guess" that the SlopeFinding function (a.k.a. the derivative) is exponential. Some will even hone in on the constant factor that appears to be the stretch factor involved. There is a wonderful exploration that leads students to discover, with very little help from the teacher, that Dx(bx) = b x 1nb. It's a little too long to include here, but ask questions if you want to know more. - Explore functions that aren't differentiable at all points on their domain. (For example,
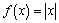 or
or 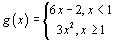 .) We use these to delve more deeply into the definition of the derivative to find where in the definition we find support for the fact that the derivative does not exist at a particular x-value on each domain. It is here that I often explain the Symmetric Difference Quotient used by the TI-83 to determine derivative values, because that calculator will actually determine a value for
.) We use these to delve more deeply into the definition of the derivative to find where in the definition we find support for the fact that the derivative does not exist at a particular x-value on each domain. It is here that I often explain the Symmetric Difference Quotient used by the TI-83 to determine derivative values, because that calculator will actually determine a value for 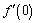 and for
and for 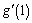 . This whole exploration raises many questions, and we often take off on tangents (no pun intended) at this point.
. This whole exploration raises many questions, and we often take off on tangents (no pun intended) at this point. - This is just a sampling of some of the exploring we do, and I hope that this outline has helped clarify why I might spend three weeks on local linearity. In these first weeks, I often (but not always) find myself introducing Newton's Method or L'Hopitals Rule as merely extensions of local linearity. We, of course, always cover using the tangent line to approximate nonlinear function values. And, thinking about tangent lines, students understand that the good linear models they have created throughout the early stages of this unit lead naturally to "tangent lines" that we define to be the best linear models (if they exist) for a function at a particular point. That "best" linear model for f at
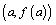 is the line that contains
is the line that contains 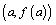 and that has
and that has 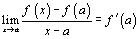 as its slope.
as its slope.
J. T. Sutcliffe holds the Founders Master Teaching Chair at St. Mark's School of Texas in Dallas. A recipient of the Presidential Award for mathematics teaching, as well as Siemens and Tandy Technology Scholars awards, she has served as a member of the AP Calculus Development Committee and as an AP Calculus Table Leader. In addition, J. T. has served on advisory and developmental boards for the College Board Vertical Team and Building Success committees and has also helped develop Pacesetter: Mathematics with Meaning, a teacher professional development project for the College Board.
Authored by
J. T. Sutcliffe
St. Mark's School
Dallas, Texas