Critical Thinking Questions in Physics
Introduction
The emphasis on conceptual understanding, problem-solving techniques, and labs in the AP Physics courses necessitates the use of a variety of audiovisual media and demonstrations for clear and in-depth understanding of the topics being discussed. Posing challenging physics questions will stimulate critical thinking skills in students. The following activities will help students better understand the concepts in the courses and should have a positive effect on their performance on the exam. These questions are focused on the following critical thinking topics:
Part 1
Units & Dimensions: 1-3
Distance and Displacement: 4-6
Kinematics and Projectile Motion: 7-13
Circular Motion: 14
Weight & Weightlessness: 15-18
Angular Momentum: 19
Electricity and Magnetism: 20-21
Part 2
Thermal Physics: 22-24
Fluid Mechanics: 25-32
Waves & Optics: 33-35
Modern Physics: 36
Critical Thinking Questions in Physics: Part 1
-
$1 = 100¢
= 10¢ x 10¢
= $(1/10) x $(1/10)
= $(1/100)
= 1¢Answer: There is incorrect use of units. In the second step, the effective unit of ¢2 is not the same as $ on the left side. Again, the unit of $2 in step 3 is changed to $ in the fourth step.
-
The Eiffel Tower has a mass of 10,000,000 kg. A 100:1 scale model of the tower made from the same material will have a mass of
- 100,000 kg
- 10,000 kg
- 1,000 kg
- 100 kg
- 10 kg
- 1 kg
Answer: (E) 10 kg
Some students may jump to the answer of 100,000 kg, thinking the model will weigh 1/100 of the actual tower. However, if the height of the model is 1/100 of the height of the tower, all its dimensions are 1/100. Hence the model is (1/100) x (1/100) x (1/100) = 1 millionth of the volume of the actual tower (no matter what shape the tower is). So if the model is made of the same material as the tower, its mass would be 1 millionth the mass of the tower, i.e., 10 kg.
-
Three men—A, B, and C—crossed paths walking through woods on a cold night. They decided to light a fire to rest by, and set out to gather some firewood. A came back with 5 logs of wood, B brought 3 logs, but C came back empty-handed. C requested that they let him rest by the fire and promised to pay them some money in the morning. In the morning C paid them $8. How should A and B split the money fairly?
- A $7; B $1
- A $6; B $2
- A $5; B $3
- A $4; B $4
- None of these
Answer: (A) A $7; B $1
All three men are equally benefited by the fire from the 8 logs of wood. Each man used 8/3 logs of wood through the night. Therefore,
A contributed 5 - 8/3 = 7/3 logs of wood.
B contributed 3 - 8/3 = 1/3 log of wood.
Therefore they must share $8 in proportion to 7/3:1/3 or 7:1.
-
An insect is climbing up a 30 ft. vertical wall. Starting from the bottom it climbs up 3 ft. during the day and slips down 2 ft. at night. In how many days will it reach the top of the wall?
- 31 days
- 30 days
- 29 days
- 28 days
- 27 days
- Never
Answer: (D) 28 days
Some students may answer 30 days, arguing that the insect gains 1 ft. in height per day. But in 27 days it will have climbed 27 ft., and on day 28 it will cover the remaining 3 ft. to reach the top.
-
A person somewhere on the earth travels 10 mi. south, then 10 mi. east, then 10 mi. north. He is back at his starting point. Which place on the earth is he?
Answer: There is one solution at the North Pole, and there are infinite solutions at the South Pole, as illustrated by the diagrams below.
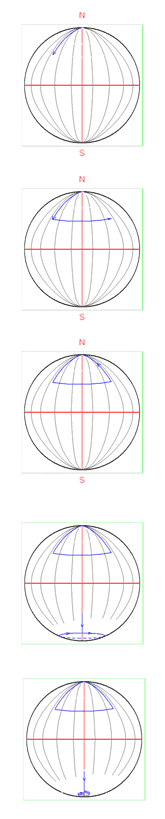
-
A hiker started to climb up a hill at 6:00 a.m. and either kept climbing up or rested at some place(s). He reached the top at 6:00 p.m. He rested there for the next 12 hours. The next day at 6:00 a.m. he began to travel down the same path. He either moved downward or rested at some place(s). For the up and down trips, how many times was he at the same place at the same time?
- Never
- At least once
- Once and only once
- At most once
- Only twice
- None of these
Answer: (C) Once and only once
Method 1: Draw the x vs. t graph for the hiker, with t ranging from 6:00 a.m. to 6:00 p.m. for the two days. The graphs for the two trips will intersect for only one value of x.
Method 2: Imagine that as the hiker starts to ascend, there is a "virtual hiker" who starts the descent at 6:00 a.m. It is easy to see that the two "hikers" will meet once and only once.
-
Mr. Fiz is returning home at a speed of 2 mph with his dog Ix. He unleashes Ix when they are still 3 miles from his house. Ix happily begins running back and forth between the house and his master with a constant speed of 3 mph. Ix does not waste any time while turning around. By the time Mr. Fiz reaches home, how many miles has Ix run?
- 3.5 miles
- 4.0 miles
- 4.5 miles
- 3.333... miles
- 3.555... miles
- None of these
Answer: (C) 4.5 miles
Some students may try to form a summation series for the distances traveled by the dog for the trips between the house and the master. It gets very complicated.
The simple solution: Mr. Fiz takes 1½ h to reach home. Therefore, the dog has been running for 1½ h. With the speed of 3 mph, the dog has traveled a distance of (3 mph) x (1½ h) = 4.5 miles.
-
A person travels from city A to city B with a speed of 40 mph and returns with a speed of 60 mph. What is his average round-trip speed?
- 100 mph
- 50 mph
- 48 mph
- 10 mph
- None of these
Answer: (C) 48 mph
The answer does not depend on the distance between the cities A and B. Assume the distance to be x, with round-trip distance 2x. The time taken from A to B is x/40 h, and the time for the return trip is x/60 h. For the speeds of 40 mph and 60 mph, the round-trip time is 2x/40 h and 2x/60 h. The average speed is defined as Vavg = total distance ÷ total time.
This becomes an exercise in the arithmetic of fractions. The answer turns out to be 48 mph, independent of x. Students are very likely to jump to the answer of 50 mph, as it is the average of the given speeds. However, that is not the way average speed is defined!
-
Two trains are moving toward each other with speeds of 17 mph and 43 mph. How far apart are they 1 minute before they pass each other?
- 60 miles
- 30 miles
- 6 miles
- 3 miles
- 2 miles
- 1 mile
Answer: (F) 1 mile
There is no need to do tedious calculation if we realize that each train is approaching the other at a relative speed of (17 mph + 43 mph) = 60 mph = 1 mile/min. Hence 1 minute before collision they are 1 mile apart.
-
Two marbles roll along two horizontal tracks. One track has a dip and the other has a bump of the same shape. Which marble wins?
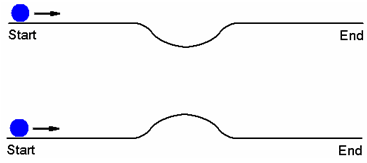
Answer: On the straight parts of the tracks the two marbles have the same speed. However, at every point of the dip the marble has greater speed than the other marble at the corresponding point of the hump. Thus the marble on the track with a dip wins. This argument assumes that the marbles always remain in contact with the tracks.
-
Three projectiles are launched from the same point over a level ground with speeds VA, VB, and VC. They all attain the same maximum height. Which of the following is true about their times of flight?
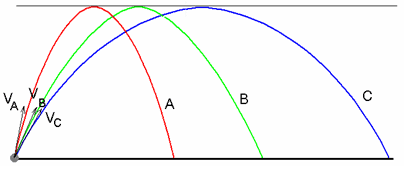
- tA = tB = tC
- tA > tB > tC
- tA < tB < tC
- None of these
Answer: (A) tA = tB = tC
The three projectiles have equal maximum heights, hence they have equal initial vertical components for their speeds. Thus they all take equal times to reach the maximum height and return back to the ground. (Students may think that since the projectiles travel different distances along their trajectories they have different travel times.)
-
Three projectiles are launched from the same point over a level ground with speeds VA, VB, and VC. They all attain the same maximum height. Which of the following is true about their initial speeds?
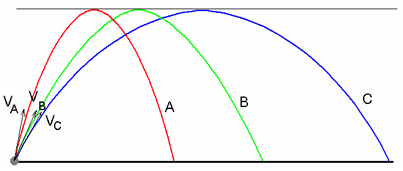
- VA = VB = VC
- VA > VB > VC
- VA < VB < VC
- None of these
Answer: (C) VA < VB < VC
The three projectiles have equal initial velocities and equal times of flight. However, for their horizontal ranges XA < XB < XC. The horizontal range is caused by the horizontal components of their speeds in the same time. Hence VAx < VBx < VCx. This implies that VA < VB < VC.
-
A ball is launched from the same height repeatedly with the same speed Vo but in different directions A, B, and C as shown below. It reaches the ground with speeds VA, VB, and VC respectively. Which of the following is true about these speeds?
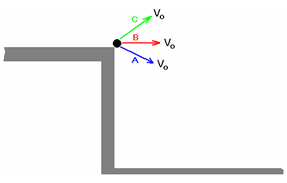
- VA = VB = VC
- VA > VB > VC
- VA < VB < VC
- None of these
Answer: (A) VA = VB = VC
In each instance, the ball starts with the same speed, hence the same kinetic energy. When the ball hits the ground, it has lost the same amount of gravitational potential energy and hence gained the same amount of kinetic energy. Thus, in each instance, the ball hits the ground with the same speed.
Here students might think that direction of the initial velocity may affect the speed of impact on the ground.
-
A drum is spinning at constant speed with its axis vertical. A drop of water at a point P on its surface detaches and flies off. Looking from the top, what is the most likely path followed by the drop?
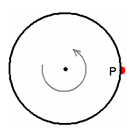
Answer: The water drop P is initially in uniform circular motion. Hence at any moment its velocity is tangential to the drum surface. When it detaches from the drum, there is no more centripetal force causing it to go in a circular path so it travels tangentially off from the surface.
In a three-dimensional picture, the drop will follow a parabolic path to the ground.
-
The weight of a closed jar is W while the flies inside it are flying around. What will be the weight of the jar if the flies settle down inside the jar?
- Equal to W
- Less than W
- Less than W
Answer: (A) Equal to W
When the flies are flying, they are pushing down on air, which in turn is pushing down on the jar. In fact, the jar is supporting the flies even when they are flying around. If the jar were placed on a sensitive scale, the reading would fluctuate about W and average out at W over a long interval of time.
-
A closed jar containing a gas is weighed. Do the molecules of the gas contribute to the measured weight?
- Yes, fully
- Yes, but partially
- No
Answer: (A) Yes, fully
This may appear to be similar to question 15. However, in this case we are considering whether the weight of the gas itself contributes to the weight of the whole system. One approach to this problem is to consider the vertical velocities of the molecules. As a molecule moves down, its velocity is increasing due to the acceleration due to gravity. When the molecule collides with the bottom of the container, it imparts a force in excess of its weight; the excess force is just right to compensate for the time the molecule was not in contact with the jar.
Again, on a microscopic scale, if the jar were placed on a sensitive scale, the reading in the scale would vary around W but average out to W over a long enough interval of time.
-
How do astronauts weigh themselves in the state of weightlessness?
Answer: The weight of astronauts in a close orbit around the earth is about 90 percent of their weight on the surface of the earth. However, they feel weightless because they are effectively in a free fall and hence have no normal force from a surface acting on them. The normal force gives people a feeling of their weight. If a person stands on a weighing scale to find her weight, the scale reads the normal force it applies to support that person. Hence a weighing scale would show zero weight for an astronaut if she "stands" on such a scale in a satellite. However, astronauts can find their mass (inertia) using the fact that the period of oscillations of a spring-mass system depends on the mass attached to it and not on the gravity. A machine designed by NASA on this principle is called a Body Mass Measuring Device (BMMD).
-
A person carrying a cup of water with floating ice steps into an elevator. If the elevator accelerates upward, the ice will
- Float higher
- Sink deeper
- Stay at the same level
Answer: (C) Stay at the same level
The upward accelerating frame is equivalent to an inertial frame with a higher value of gravitational acceleration given by g' = g + a. The buoyancy force on the ice is due to the pressure of water, which is proportional to gravity g'. The weight of the block is mg'. Hence both the weight of the block and the buoyancy force increase by the same factor when the elevator accelerates upward (and decrease by the same factor when the elevator accelerates downward). Therefore the ice floats at the same level and the level of water in the cup does not change.
-
Why does a helicopter have a second propeller near its tail?
Answer: As the main (horizontal) propeller rotates one way, the rest of the helicopter tends to rotate in the opposite direction due to the law of conservation of angular momentum. The rotation of the main body of the helicopter can be prevented by another propeller near the tail of the helicopter.
-
There are three switches A, B, and C in a room. Two of them are dummy switches, and the third is the switch for a desk lamp in another room. You are allowed to turn the three switches on and off as you like. You then go into the room with the desk lamp only once, and you are able to tell which of the switches is the right switch for the lamp. How can you do this?
Answer: Turn switch A on. Leave it on for a few minutes. Turn A off and B on. Go to the desk lamp.
If the lamp is on, it is B.
If the lamp is off and the bulb is warm to touch, it is A.
If the lamp is off and the bulb is cool to touch, it is C.
-
A boy carries a metal rod PQ horizontally on a pickup truck traveling on a straight horizontal road. An emf is induced in the rod due to the earth's magnetic field, making the end P positive (+) and the end Q negative (-). The ends of the rod are now connected by a wire. In which direction will the induced current, if any, flow in the rod?

- P to Q
- Q to P
- No current will flow through the rod.
Answer: (C) No current will flow through the rod.
The rod and the wire form a closed loop. There is no change in the magnetic flux through the loop as the truck moves along a straight line. Hence, by Faraday's law, there is no induced emf or induced current in the loop.
Critical Thinking Questions in Physics: Part 2
-
Two identical cups P and Q have equal amounts of hot coffee at the same temperature. Cold creamer is now added to the cup P. A few minutes later, the same amount of cold creamer at the same temperature is added to the cup Q. Compare the new temperatures TP and TQ of the coffee in the two cups.
- TP = TQ
- TP > TQ
- TP < TQ
Answer: (B) TP > TQ
This is a question on heat transfer and Newton's Law of Cooling. A body at a higher temperature loses heat to the surrounding area at a higher rate. Since the cup Q was left at a higher temperature for a longer time interval, it has lost more heat.
-
A metal rod AB is bent into the shape shown.
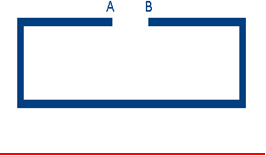
If the rod is heated uniformly, the space between the ends will
- Increase
- Decrease
- Stay the same
Answer: (A) Increase
In thermal expansion of an object of any shape, every particle moves away from every other particle. If the points A and B move closer, it will be contrary to expansion.
The straight sections ending in A and B do expand and cause the points A and B to come closer. However, the expansion of the lower straight segment moves the points A and B apart. The length of the lower segment is greater than the total length of the two upper segments. Hence the net effect is that the points A and B move farther apart.
-
A container is divided into two halves by a partition with a hole in it. The two halves contain the same gas but at different temperatures. Which half, if any, contains a greater amount of gas?
- The half at higher temperature
- The half at lower temperature
- The halves contain equal amounts of the gas.
Answer: (B) The half at lower temperature
The answer can be quickly found using the well-known equation PV = nRT. The hole in the partition causes the pressure to be the same in both halves. Hence the number of moles
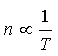 .
. -
A bottle is filled completely with water, as shown in the diagram below. Which of the points shown have the same pressure?
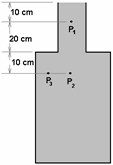
- P1 and P2
- P2 and P3
- P1 and P3
- P1, P2, and P3
- None of these
Answer: (B) P2 and P3
The pressure due to a liquid at a point is proportional to the depth of the point below the open surface of the liquid. This is true even if the open surface is not vertically above the point, as is the case with the point P3. One might think that P1 and P3 have the same pressure, as both of them are 10 cm below the surface of the liquid. This not true because the water surface directly above P3 is not an open surface.
-
Two identical beakers hold water at the same height, but one of them has a wooden block floating in it. Which beaker, if either, weighs more?
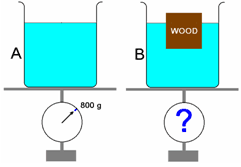
- A
- B
- Neither
Answer: (C) Neither
The amount of water in the beaker B is less than that in A due to the water displaced by the floating block. However, applying the Archimedes principle, the weight of the floating block is equal to the weight of the water it has displaced.
-
Two identical beakers hold water at the same height, but one of them has a block of wood immersed completely and attached by a string at the bottom. Which beaker, if either, weighs more?
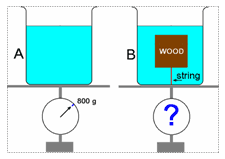
- A
- B
Answer: (A)
In the beaker B, the displaced volume of water has been replaced by the wooden block of lesser density. Hence it weighs less.
-
Two identical beakers hold water at the same height, but one of them has an iron block immersed in it. Which beaker, if either, weighs more?
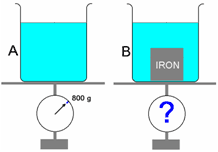
- A
- B
- Neither
Answer: (B)
In the beaker B, the volume of displaced water is occupied by the iron block of greater density. Hence it weighs more.
-
Two identical beakers hold water at the same height, but one of them has an iron block suspended in it by a string. Which beaker, if either, weighs more?
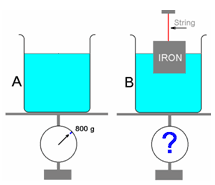
- A
- B
- Neither
Answer: (C) Neither
Beaker B is missing water displaced by the partly immersed iron block. The buoyancy force on the block equals the weight of the water displaced. This force also acts on the bottom of the beaker as a reaction force and compensates exactly for the reduction in the weight due to missing water.
-
Two identical beakers hold water at the same height, but one of them has a completely immersed iron block suspended in it by a string. Which beaker, if either, weighs more?
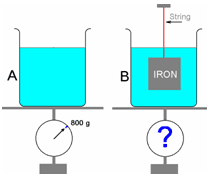
- A
- B
- Neither
Answer: (C) Neither
In beaker B, the iron block experiences an upward buoyancy force equal to the weight of water displaced. The buoyancy force is applied by the water upward on the block and as a reaction downward on the bottom of the beaker, thus compensating for the weight of the displaced water.
-
A boat in a lake drops an anchor into the lake. The level of the lake will
- Remain the same
- Rise
- Fall
Answer (C) Fall
When in the boat, the anchor displaces water equal to its own weight. Since the density of the anchor is greater than the density of water, the volume of water displaced is greater than the volume of the anchor. When the anchor is dropped in water, the anchor displaces volume equal to its own volume. Hence the volume of water displaced when the anchor is dropped in the lake is less than when the anchor was in the boat, and the level of the lake falls.
-
A 2-ton boat is floating in a lake. The buoyancy force on the boat must be
-
- 2 tons
- More than 2 tons
- Less than 2 tons
- Dependent on the density of water in the lake
Answer: (A) 2 tons
When in the boat, the anchor displaces water equal to its own weight. Since the density of the anchor is greater than the density of water, the volume of water displaced is greater than the volume of the anchor. When the anchor is dropped in water the anchor displaces volume equal to its own volume. Hence the volume of water displaced when the anchor is dropped in the lake is less than when the anchor was in the boat. Thus the level of the lake falls.
-
When we look at ourselves in a plane mirror, we see left-right reversal but not up-down reversal. Why?
Answer: There is depth inversion and no left-right inversion in a plane mirror. Right appears right, left appears left, up appears up, and down appears down. However, to a person looking into the mirror, there is an illusion of left-right reversal and no up-down reversal. This is due to the fact that for another person to face the observer, the other person always turns around a vertical axis, causing a real left-right reversal.
-
The wavelength of red light is close to blue in water, yet the red exit signs appear red to a swimmer from inside water. Why?
Answer: When light enters a medium from another medium, its wavelength and speed change, and frequency stays the same. The wavelength in the second medium is not affected by the introduction of a third medium between the two mediums. Thus red light entering the eye directly from air has the same wavelength inside the eye as the red light first entering water then into the eye, so red light appears red to a swimmer under water.
-
Our eyes are most sensitive to greenish-yellow light, yet the danger signals are red. Why?
Answer: Red light can penetrate through atmosphere containing dust, clouds, and fog much more efficiently than any other color. Light toward the blue end of the visible spectrum is scattered to a much greater extent by the atmosphere. That's why the sky appears blue, and sunset and sunrise skies are reddish.
-
Why can't the electron-positron pair-production take place in a vacuum?
Answer: Pair-production is the creation of an electron-positron pair by a gamma ray photon. In this process, the photon disappears and its energy is converted into the rest mass of the electron-positron pair and the kinetic energy they carry. A portion of the energy of the photon is turned into the rest mass of the electron-positron pair. Thus the linear momentum of the pair is less than the momentum of the photon; this is violation of the law of conservation of linear momentum. Hence the pair-production always takes place in the vicinity of a heavy nucleus. The recoil of the nucleus ascertains conservation of linear momentum.
Authored by
Hasan Fakhruddin
The Indiana Academy for Science, Mathematics, and Humanities BSU
Muncie, Indiana