AP Physics Featured Question: Projectile Concepts
Introduction
My students pretty quickly become comfortable with algebraic kinematics problems, even those in two dimensions. The mathematical process is soothing to the psyche: each problem seems to be a variation on the same theme, thus building confidence with every correct numerical answer obtained.
But how to check my class's conceptual understanding? Knowing what kinematics calculations mean is ultimately as important as being able to do the calculations to begin with. In that spirit, here's a different sort of projectile question, the kind that's rare to see as an end-of-chapter exercise. Not a single calculation is necessary, yet I'd in no way categorize it as easy compared with typical AP questions.
This problem correlates to Learning Objective A.2 in the Course Description: Motion in two dimensions, including projectile motion.
AP-Style Problem with Solution
Jim and Sara stand at the edge of a 50 m high cliff on the moon. Jim extends his arm over the cliff edge and throws a ball straight up with an initial speed of 20 m/s. Sara throws an identical ball with the same initial speed, but she throws the ball at a 30 degree angle above the horizontal.
-
Consider each ball at the highest point in its flight. At this point:
-
Which ball has the greater vertical velocity? Choose your answer and explain briefly.
Answer:
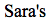
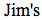

The highest point in any ball's flight is when its vertical velocity changes direction from upward to downward and thus is instantaneously zero.
-
Which ball has the greater horizontal velocity? Choose your answer and explain briefly.
Answer:

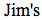
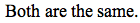
The horizontal velocity of Jim's ball is zero throughout its flight, because it doesn't move horizontally. Sara's ball maintains its initial horizontal velocity throughout its flight, including at its highest point.
-
Which ball's velocity vector has greater magnitude? Choose your answer and explain briefly.
Answer:

The magnitude of the velocity vector is determined by the Pythagorean sum of the vertical and horizontal velocity vectors. Jim's ball's velocity is zero in any direction; Sara's ball has a nonzero horizontal velocity and thus a nonzero vector velocity.
-
-
Now consider each ball just before it hits the ground, 50 m below where the balls were initially released. At this point:
-
Which ball has the greater vertical velocity? Choose your answer and explain briefly.
Answer:

Consider each ball at the peak of its flight: Jim's ball goes much higher than Sara's because Jim gives his ball a much bigger initial vertical velocity. For this question, then, we can compare the vertical velocity of two balls dropped straight down from different heights. Obviously the ball dropped from the higher height moves faster upon hitting the ground, so Jim's ball has the bigger vertical velocity.
-
Which ball's velocity vector has greater magnitude? Choose your answer and explain briefly.
Answer:

The magnitude of a velocity vector is better known as the scalar quantity speed. For two identical balls, the one with more kinetic energy also has more speed. The total mechanical energy of each ball is conserved, because no nonconservative force (such as air resistance) acts. Both balls travel from the top of the cliff to the ground, losing identical amounts of potential energy in the process. By conservation, then, both balls must gain identical amounts of kinetic energy, increasing their speeds by the same amount.
-
-
Which ball reaches the peak of its flight more quickly after being thrown? Choose your answer and explain briefly.
Answer:

Consider only the balls' vertical motion. Sara's ball has a smaller initial vertical velocity, but both balls slow down with the same acceleration. So Sara's ball will get to zero speed (the peak of its flight) sooner.
-
Below is a velocity-time graph representing the vertical velocity of Sara's ball. On the same axes, sketch a velocity-time graph representing the vertical velocity of Jim's ball.
Answer (blue line):
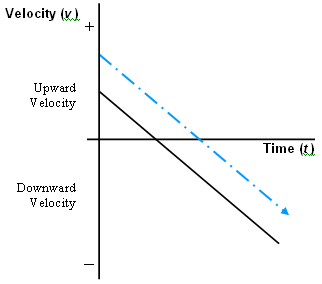
Jim's ball has a larger upward vertical initial velocity, so its v-t graph starts higher up on the v-axis. But since both balls have an acceleration equal to g, the slope of both lines will be the same. (The dotted blue line should go on the graph itself. The line should start on the vertical axis, and should be parallel to the original line.)
Commentary
-
When asked to explain an answer, students should do so concisely. On the AP Exam, writing more than a few sentences wastes time and puts a student at risk for losing points. If the first four sentences are correct, but a fifth sentence is factually incorrect, the answer will not receive full credit.
-
On that note, if a free-response question says to choose one and explain, students should at least choose one, even if they have no clue, even if they are running out of time. Invariably, they will earn some small amount of credit just for guessing right.
This does NOT mean that "gaming" the exam is possible or a useful general strategy. For one thing, students can earn no more than a very few of the 80 to 90 points available on the free-response section simply by checking the correct box. Random guessing by itself won't even get students a 2 on the free-response section. If a student is running out of time, though, a few random guesses might give him or her the extra couple of points needed to bump up the score.
More to the point, guessing correctly often involves a physics instinct as well as pure randomness. A good physics student does develop an intuition about how the natural world works and so can sometimes understand some aspects of a topic without being able to eloquently verbalize why he or she knows it. This is the reason I tell my students to always guess at an unknown answer to a multiple-choice question.
-
Read the question. A large number of my students, even my very bright students, don't notice that part (a) asks only about the ball at the highest point in its flight.
-
On a similar note, one would expect that part (a)(iii) is redundant. Anyone who knows that the peak of flight means no vertical velocity should obviously also recognize that Sara's ball is the only one that's moving, right? Well, no, unfortunately. Some students rush through the problem, seize on their recognition that "magnitude of the velocity vector" means speed, and note that speeds are the same—without any thought to where in the flight is being considered. Other students don't really understand the language here: "magnitude of the velocity vector" may as well be written in Greek. There's little a teacher can do about the former mistake, other than dock credit; the latter mistake represents a teaching opportunity. Perhaps those who don't know what the word "magnitude" means might use this problem to figure it out.
-
A fair number of students draw the graph of Jim's ball so that it intersects the t-axis at the same place Sara's does. The misconception there is explored in question 2 of the follow-up quiz I've provided: even though both balls have the same vertical velocity of zero at the peak of their flight, that doesn't mean that both balls hit the peak of flight at the same time. And, no matter how many times you remind your students that the slope of a velocity-time graph is acceleration, they won't all think in terms of matching the graphs' slopes.
-
Ah, the everlasting student hang-up: "Can I use 10 m/s2 for g? Isn't 9.8 m/s2 more accurate?" I point out that the difference between the two values is 2 percent. I tell the class: pretend that the answer to a homework problem is, say, 4.4 m. But suppose you round numbers differently, or use an incorrect number of significant figures, and get an answer of 4.49 m. Do you want me to count this as correct? Or, do you want me to dock credit for failing to match my answer? (The students' preference should be obvious to all readers.) Well, 4.49 m differs from my answer by 2 percent: close enough for my class, and close enough for the AP Exam.
Problem Posed Quantitatively as a Homework Assignment
On an airless planet the same size and mass of the Earth, Jim and Sara stand at the edge of a 50 m high cliff. Jim extends his arm over the cliff edge and throws a ball straight up with an initial speed of 20 m/s. Sara throws an identical ball with the same initial speed, but she throws the ball at a 30 degree angle above the horizontal.
-
Determine the horizontal and vertical components of each ball's velocity when it is at the highest point in its flight. Then, determine the magnitude of each ball's velocity vector at the highest point.
-
Determine the horizontal and vertical components of each ball's velocity when it reaches the ground, 50 m below where it was initially thrown. Then, determine the magnitude of each ball's velocity vector at ground level.
Follow-Up Ideas
-
How can you measure the horizontal and vertical velocities of a projectile? Vernier's Logger Pro can import video of a projectile. From the video, you can produce graphs and calculations of pretty much any quantity you want. Experimentally verify the answers to the AP-style problem above. Take video of two balls, perhaps launched with a Pasco projectile launcher so they are guaranteed to have the same initial speed. Launch one ball straight up, the other at an angle. Import the video to Logger Pro. Then check to see whether the speed of each ball is in fact the same at a given height.
-
Consider the scale of this experiment. The ball is thrown with a speed of 40 to 45 miles per hour. How fast is that? At a spring training baseball game, I saw a boy of about 10 throw in the 45 mph range on the novelty radar gun.
The cliff in question is 50 m high, which is about the height of a 15- to 16-story building, or half a football field.
Neglecting air resistance, the ball ends up at the bottom of the cliff with a speed of 37 m/s, or about 80 mph—so this 10-year-old boy could pitch in the major leagues if he could throw off a 150-foot mound. (The pitcher's mound is, in fact, 10 inches above the playing surface.)
-
Projectile Motion applet: This applet lets you specify the speed, angle, and mass of a projectile launched on level ground. Why would you bother to specify the mass, since mass does not affect the flight characteristics of a projectile? Well, this applet lets you choose to include or ignore air resistance. You'll see that, even for fast speeds, a massive cannonball's range is reasonably close to that predicted by vacuum kinematics; but a 1 kg mass (the smallest allowed by the applet) takes a path that looks enticingly similar to the trajectory shown in golf-ball commercials, and it comes nowhere close to the vacuum range.
Follow-Up Quiz with Solutions
You may use your original projectile problem, including any notes you made on it, as a reference.
-
Why does the problem state that Jim and Sara are on the moon?
Answer: On the Earth, a ball will approach its terminal velocity after falling for 50 m (about 15 stories). The assumption of constant acceleration, necessary for using standard kinematics, would not be valid. Since the moon has no atmosphere, though, a kinematics approach is fine.
-
Answer in no more than three words: how do you find acceleration from a velocity-time graph?
Answer: Take the slope.
-
If these balls were thrown from the 50 m high cliff on an airless planet of the same size and mass as the Earth, what would be the slope of a graph of the vertical velocity of Jim's ball vs. time? Answer in units of m/s2.
Answer: 10 m/s2
-
Both balls are thrown with the same initial speed. One can use conservation of energy or kinematics to show that both balls still have the same speed when they hit the ground, no matter how far the ground is below the cliff. So how is it possible that the balls have different speeds at the peaks of their flights?
Answer: The balls start with the same kinetic energy. If the balls undergo the same change in potential energy, they will still have the same amount of kinetic energy. The balls are at different heights when they reach the topmost point in their flights—Jim's ball is higher. Since potential energy depends on height, Jim's ball will have gained more potential energy and thus lost more kinetic energy and speed.
-
Could be tough: show using kinematics that the speed of both balls is the same after the balls have fallen a vertical distance y.
Answer: Let the initial speed of each ball be v0. The positive direction will be up; thus both g and y come with a negative sign, and v0 is a positive quantity.
Jim's ball:
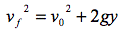
Sara's ball (vertical component):
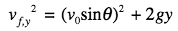
Sara's ball (horizontal):
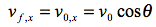
We now have the final speed vf of Jim's ball. To get the final speed of Sara's ball, add the horizontal and vertical components of the velocity vectors of Sara's ball using the Pythagorean theorem:
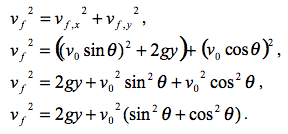
Now we recall the "Great Truth of Mathematics":1
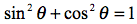 . We can see that the speeds of both balls upon hitting the ground are given by the same equation:
. We can see that the speeds of both balls upon hitting the ground are given by the same equation: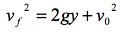
[You can also see this calculation, done with values plugged in, in the solution to the quantitative homework problem.]
Note
1 This moniker courtesy of Gregg Musiker.
Authored by
Greg Jacobs
Woodberry Forest School
Woodberry, Virginia