Why We Use Theorem in Calculus
As teachers of mathematics, we understand how theorem and proof provide the underpinnings of the complex processes that form calculus techniques. However, the students who study the subject often view calculus as consisting mostly of processes and some quantitative calculations, independent of and unrelated to the axioms and theorems underlying the results. This paper presents my opinions and some evidence as to why we do and should emphasize theorem in the teaching of calculus.
A story I am fond of retelling is getting to know the businessman husband of a friend of mine. When he discovered that I am a mathematician, he exclaimed that he recalled the Fundamental Theorem of Calculus from his college studies some 20 years earlier. "Why, that is how you can get a speeding ticket on a toll road just from your clocked ticket-in and ticket-out," he proudly exclaimed. Although he has the names of the Mean Value Theorem and the Fundamental Theorem confused, the power of the underlying mathematics remained with this friend long after our manipulative analytical techniques had worn off. It is my opinion that a sense of the strength and power of mathematics should be a goal of any calculus course, and using theorem is an excellent way to develop this sense.
Of course, when we as mathematicians teach the Fundamental Theorem of Calculus, we can't help saying "Ain't it great?" We marvel at the two-sided link of the differential and integral calculus. But just that marvelous synchronicity isn't a sufficient reason to teach calculus to the hundreds of thousands of students who encounter it each year. We have to choose what to teach and how to teach it according to the needs and learning objectives of our students.
Designing a Course that Meets Your Students Needs
In order to examine our curriculum and determine the essential elements of a successful calculus course, we must consider each of the interacting components: environment and audience, course outcomes, required content, synthesizing the content delivery with other goals (such as developing communication skills), and assessing understanding. To begin, an understanding of our classroom audience is essential to the success of any mathematics course. "Audience" is a misnomer, since of course we really aim to have "participants" or "learners." We should be designing our calculus curriculum for the majority of our students. Who these students are varies from school to school, and the experiences differ of high school calculus students from that of students enrolled in college. The budding mathematicians in the calculus course are, alas, few and far between. We should hope that a well-designed curriculum will help them to continue successfully on their chosen path while ably serving a larger clientele. In this paper, we will assume that the student who is prepared for calculus is reasonably skilled at algebra, trigonometry, and the rudiments of function, while also enrolled for a variety of reasons.
Let us investigate the reasons for young students to choose to enroll in AP Calculus, and determine how a successful calculus course can help those students develop skills necessary for their future education. In turn, examining the needs of our participants can help us to define achievable course objectives. The student enrolled in AP Calculus has chosen to get a head start on the mathematics requirements for college. Successful completion of the course and exam will earn the students credit at most colleges. Many of these students will actually use calculus tools for advanced studies in their undergraduate science career. For example, they are expected to model and evaluate definite integrals, perform integration by parts, estimate series, or choose appropriate curves to fit data. It is true that students often need to be reminded at that later date of the actual calculus manipulations. However, we hope that they do have the necessary habits of mind that allow them to understand the nature of the mathematical problem involved and sufficient facility with the material to research and implement correct solution methods. In my opinion, spending class time on the study of theorem in calculus will help these students develop those habits of mind. For other liberal arts and sciences students, calculus study can develop reasoning skills, understanding of the concept of rigorous derivations of theorems and proofs, implementation of problem solving strategies, and communicating understanding of technical matters. The examples of the study of theorem below will illustrate how we can make sure these students develop such skills in calculus.
When designing the mathematics curriculum, we often have a content list in mind. However, there are skills and development objectives within each mathematics course that extend beyond familiarity with content and preparation for a next course. From general mathematics objectives, we can distill calculus objectives. We approach topics via the "rule of 4" so as to ensure the student can address problems in both mathematics and other disciplines from multiple avenues. We hope to instill good number sense and develop both logic skills and reasoning. Students do need some drill exercises so that they can accurately use the tools to solve problems. Through this work they should develop an appreciation for the idea of using the right tool and having a basic skill set. With all these objectives in mind, there are certainly multiple goals for each teaching session. Using the study of theorem is more suited to some of these goals than others. Finding the right blend of skill, drill, theory, and common sense to develop a successful student is the ultimate goal of the teacher who hopes to do more than just cover five chapters of content in the time allotted. Finally, we hope the student will get a good sense of how calculus fits together—the big picture. Let us see how the study of theorem can help this happen.
The Intermediate Value Theorem
The Intermediate Value Theorem is particularly important in the development of young mathematics thinkers. This is one of the first theorems that students encounter of the form "If p, then q." In preparatory coursework for calculus, most theorems are of the form "p, if and only if q" or restatements, replacing equal items for equal items. Think of the Factor Theorem, for example, which equates roots of polynomials with factors. Or consider the Pythagorean identities in elementary trigonometry, which restate the Pythagorean Theorem. But the Intermediate Value Theorem requires the student to use Modus ponens to make inferences about the values between the endpoints of a continuous curve. Furthermore, it is an existence theorem that is not constructive, so the inference about "c" is difficult for students to grasp. A graphing technology is useful for illustrating the theorem. We begin with just the endpoints plotted, a colored band spanning the y-values in the range. Then a particular function can be graphed, and it is great if the function values actually exceed the range of the band. The guarantee of intermediate values is by no means a restriction on the possible y-values of the function, which requires students to grapple with the distinction between a universal statement and a particular example. The theorem can be used to further develop the idea of inverse images of functions, since the intermediate value "N" implies the existence of at least one preimage "c", although there may be several.
Figures 1 and 2 below demonstrate how a graphic illustration of the Intermediate Value Theorem can help students understand. Figure 1 shows the premise of the theorem for the domain [a, b] = [-3,3]. The shaded band represents the intermediate values guaranteed to be achieved by the theorem. Figure 2 includes a particular function which satisfies the hypothesis of the theorem. This is a nice choice of function, since additional y-values are achieved, beyond those guaranteed by the conclusion of the theorem, and some intermediate values correspond to several preimages "c". Additional images to include in a student discussion should incorporate graphs where the functions have discontinuities, to demonstrate the necessity of the hypothesis and the fact that some, but not necessarily all, y-values will be excluded if the hypothesis is not valid.
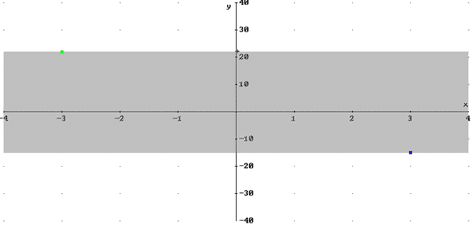
Figure 1: The Intermediate Value Theorem
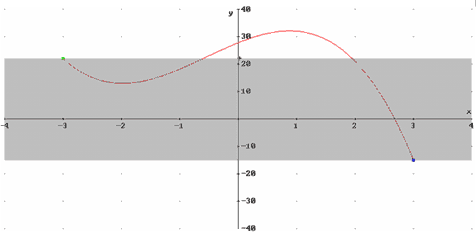
Figure 2: A function that satisfies the hypothesis
The Intermediate Value Theorem has some nice direct applications that are relevant to technologically savvy students. They are accustomed to graphing functions on their calculators, and a discussion of the way the calculator is creating this approximate image is appropriate. A quick zoom will reveal that the calculator is limited by its pixels and that line segments are not always the best way to "connect the dots." That the calculator dots are often connected across discontinuities (such as vertical asymptotes) serves to illustrate the assumptions inherent in the calculator plotting code: the program assumes that the function is continuous on a closed domain. Similarly, the classic bisection method of finding roots uses the Intermediate Value Theorem to infer the relative location of the root. This illustrates what is going on in the calculator's black box when students use handheld technology to compute a root or an intersection. It is fun to discuss how the theorem can help us prove that at some moment (in our infancy) our weight in pounds matched our height in inches.
As part of the assessment of student understanding of the theorem, I usually ask the student to first explain why the Intermediate Value Theorem may be applied to the graph in Figure 3. Then I either ask the student to provide a list of all intermediate values guaranteed by the theorem, or I select an appropriate intermediate value and ask the student to locate the corresponding input "c". What I find is that a thorough discussion of relevant graphs allows students to identify the intermediate values and find "c" with a fair degree of success. The point where students experience difficulty is in explaining why the theorem is applicable in the first place. A typical answer to this question of why the theorem applies is "because I could find the "c." Discussion of graphs where the theorem does not apply is helpful, but the Modus ponens nature of the theorem is difficult for students to grapple with. So we have several wonderful reasons to use the theorem in the classroom: it illustrates what is going on in their calculator, we help them develop logical understanding of formal implication statements, and we help them comprehend the need to understand the hypothesis component of a theorem.
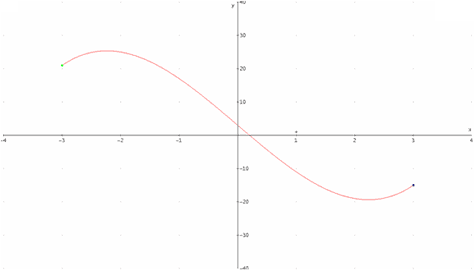
Figure 3: Intermediate Value Theorem Assessment
On [-3,3], what is the range of intermediate values guaranteed by the theorem?
The Mean Value Theorem and Rolle's Theorem
Having experienced some student confusion as to the hypothesis and conclusions of the Intermediate Value Theorem, successfully introducing the Mean Value Theorem is the instructor's next big challenge. However, the students who have spent some time studying the logic behind the Intermediate Value Theorem are better prepared to handle the logic of another "if, then" implication statement. The Mean Value Theorem is a powerful application of the differential calculus, in its meaning and applications. Presented as a graphical theorem (a secant and tangent line are parallel) together with its analytical meaning (the average rate of change is achieved as an instantaneous rate), this theorem offers a wonderful opportunity to tie graphics and analytical understanding together. Its power is revealed in applications. We can finally prove analytically that the student's common sense understanding of mathematics is correct: when a function has positive derivative, the curve must increase. This is a first instance where the student witnesses that a powerful theorem will have several important corollaries. Showing that a car must travel at exactly 45mph at least once on a one-hour, 45-mile trip is is so powerful that it remains in the student's mind for 20 years, as evidenced by the opening anecdote. And we can confirm that the student's intuition on working with antiderivatives is correct; there is just one general answer.
Once again, it is helpful to use a graphing device to look at several graphs until the students themselves identify whether the theorem applies and locate the "c" value where the tangent is parallel to the secant. Studying the Mean Value Theorem after the Intermediate Value Theorem should reveal an increase in student understanding of the logic of a theorem. They should have less difficulty with the "if, then" format, be more comfortable with the idea that the theorem does not always apply, and know what may or may not be concluded if the hypothesis is void. It is interesting to note that the hypothesis of the theorem varies from text to text. Stewart's texts require the function to be differentiable on the interval [a, b], while Larson and Thomas require the weaker condition of continuous on the closed interval and differentiable on the open set. An informal survey of 12 more calculus texts in my office, from Apostol to Ostebee-Zorn, found only one other variation from the traditional weaker hypothesis.
Depending on time constraints in the selection of content, it is interesting to first develop Rolle's Theorem in class and then prove the Mean Value Theorem from it. Rolle's Theorem follows immediately from Fermat's result that "What goes up must come down," so it provides confirmation of one's common sense. It is also nice to show that Rolle's Theorem is a special case of the Mean Value Theorem. The Mean Value Theorem for Definite Integrals is also a direct application of the Mean Value Theorem, and it has a lovely graphical interpretation in addition to its analytical form. Where the Mean Value Theorem invokes parallel line segments as a result on rates, the Mean Value Theorem for Definite Integrals invokes matching areas as a result on accumulation. Completing the proof as a straightforward application of the Mean Value Theorem serves to reinforce the primary theorem and emphasize that the power of a theorem may lie in interpolation to similar results. The Mean Value Theorem for Definite Integrals also is highly useful, in averaging functions (such as inventory models) and root mean square measurements.
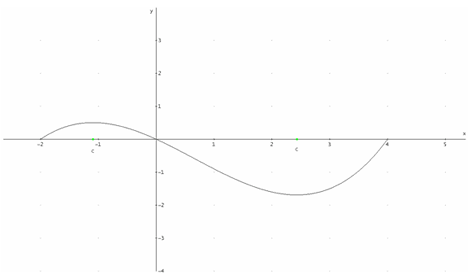
Figure 4: Rolle's Theorem as "What goes up must come down" (and vice versa)
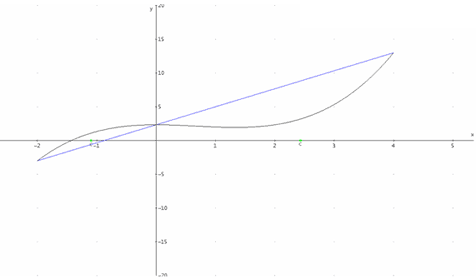
Figure 5: The Mean Value Theorem as Rolle's Theorem with your head at a tilt.
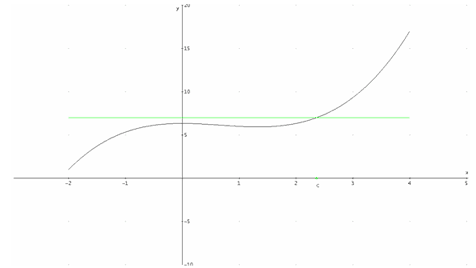
Figure 6: The Mean Value Theorem for Definite Integrals as "Cut equals fill on a hill."
The "Ta-Da" Moment of Calculus—The Fundamental Theorem
When we arrive at the "ta-da" moment of calculus, the Fundamental Theorem, our earlier work emphasizing the logic, reasoning, and rigor of theorem should yield dividends. We can logically expect that students will at that point regard the heuristic of the theorem; that the slope of the area measuring curve is the original function and the area under a curve can be found by a process that reverses the slope measurement, as a reasonable result. And whether the proof uses the definition of the derivative and the Squeeze Theorem for limits or implementation of the Mean Value Theorem, students should not be surprised that powerful previous theorems are the tools to generate the new proof. My students generally have more trouble with the process involved in implementing the First Fundamental Theorem (differentiating an area-measuring function) than with the reasoning of the proof. They suspect the process ("Really? I only have to write f(x)?") but understand the steps of the proof. The rigorous foundations of the rest of the course have made the students value the logical reasoning in the development of the calculus. And those foundations should help the students value the synchronicity of the Fundamental Theorem and exclaim "Ain't it great" right along with us.
Whether the students take one calculus course or several, the Fundamental Theorem of Calculus is significant only after developing the understanding of the logic and mathematics underlying the theorem. Deeper theorems of subsequent courses rely on those underpinnings. Through the study of various theorems in calculus, we can achieve the goals of mathematical learning: development of reasoning and communication skills, understanding of rigor, and the ability to implement problem solving strategies. Through theorem we can offer a peek into the world of advanced mathematics, its format and rigor, while achieving those goals.
References
Apostol, Tom, Calculus, vol. 1, 2nd ed., Blaisdell Publishing, 1967.
Kutzler, Bernard, "DERIVE: The future of teaching mathematics," The International Journal of Computer Algebra in Mathematics Education (formerly The International DERIVE Journal), vol. 1, no. 1 (1994), pp. 37-48.
Larson, Ron, et al, Calculus of a Single Variable (early transcendental functions volume), 3rd ed., Houghton Mifflin Company, 2003.
Ostebee, Arnold, and Paul Zorn, Calculus: From Graphical, Numerical, and Symbolic Points of View, vol. 1, 2nd ed., Brooks/Cole Publishers, 2002.
Rich, Al, and David Stoutemyer (1998), Derive for Windows, versions 4.11 through 6.0. Available through Texas Instruments at www.ti.com.
Stewart, James, Calculus: Concepts and Contexts, 2nd ed., Brooks/Cole Publishers, 2001.
Thomas, George, et al, Thomas' Calculus, (early transcendental volume), updated 10th ed., Addison Wesley, 2003.
Lisa Townsley is professor of mathematics at Benedictine University in Illinois. Her research interests include group cohomology and technology enhancement of mathematics instruction, using the software MAGMA for the former and for the latter, DERIVE and graphing calculators.
Authored by
Lisa Townsley
Benedictine University
Lisle, Illinois