Seeing Is Believing
Changed by the AP Reading
My first AP Calculus class was a group of 11 students; the school year was 1975-1976. I had not had the best experience with calculus courses as a student, and my college professor had suggested that I switch to a major in music! I wanted to do well by those 11 students, but I had to spend most of the preceding summer and then three or four hours each day that year preparing the next day's lesson. There was a lot for me to learn, and few folks around to help. The first year went well—considering—and each year I became more confident and more competent. I was a much different teacher then than I am now, however. My students fared well on the AP Examinations, but they and I focused on calculus skills since that was what the textbooks, the exams, and even the colleges were encouraging and expecting. I was proud of giving my students a rigorous, challenging course. I proved most theorems in those early days (although I didn't really understand them very well and my students got very little out of the presentations I did on the overhead—the only way I could get through many of the proofs).
Two years later I was asked to an AP Reading (if my memory serves, there were a total of 45 Readers and Table Leaders that first year). On the plane to New Jersey (and then on the way to Rider College), I was horrified by what I was doing. I was going to a place where everyone was a scholar. They would quickly "find me out" and discover that I had much to learn. Fortunately for me, I had agreed to go before what I was doing hit me. Accepting the invitation to read turned out to be a major turning point in my career and has affected, in very positive ways, not only me, but also countless students of mine and even some colleagues.
At the Reading, I found friends and mentors. No one laughed at my questions; in fact, they encouraged mine and added some of their own. I not only enjoyed getting to know them as people but also learned much mathematics from them via discussions I had with my table partner as we read student papers and discussions during our evening social hours. In the early 1980s, I started attending College Board AP workshops and doing some consulting. My original mentors continued mentoring, and new mentors were added. Preparing for workshop talks and implementing the ideas that others had shared in my classroom allowed me to continue to deepen my understanding of calculus. Along the way, there came both the calculus reform movement and graphing calculators. Suddenly, many of us realized that we wanted students to know and to value much more than the skills associated with calculus. Just when I thought I was getting a solid grip on concepts, I saw them in new ways—again thanks to mentors, institutes, Reading conversations, etc. I was energized and excited about sharing these new insights. In the classroom, I stopped proving every theorem, and I stopped asking students to do the nastiest of skill problems to "prove their competence." Instead, we focused on concept and developed skills as tools of the trade.
These days, most of my students still do well on AP Examinations, but more importantly, they have a deeper understanding of the concepts than previous students had. Now, they can connect concepts and apply them with greater confidence. They have even been known to say "Wow!" (or the equivalent) when the power, the beauty, or even the simplicity of some concept registers for the first time.
The AP Program, its people, and its professional development components have made a huge difference in my life. In turn, my deeper understanding of the concepts and my sounder pedagogical instincts have affected others, especially my students. This talk focuses on only a few examples from a list of nearly countless things I have learned along the way. Each example reinforces my belief that "Seeing is believing!"
The Derivative
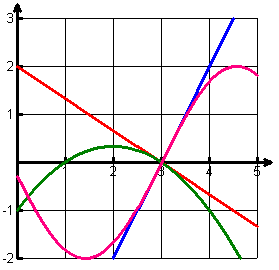
Suppose that the first thing students saw on day one of their calculus class was the following:
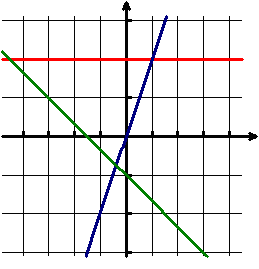
Suppose, too, that they were asked to write rules for the three functions whose graphs were sketched on the grid.
In fact, this is the way I have started my calculus classes in recent years. I always hope that someone will ask immediately about the scale of the graph, and if that question arises, I answer that the scale unit on each axis is one—the very scale most students are less than judiciously assuming to be correct. The class discussion that follows always gives me great insight into where my new students are (or are not) in their development of linear functions.
Most will give correct answers based upon the assumption of a scale unit of one for each axis and on the assumption that the graphs are those of linear functions. The more typical errors do occur, however, such as "redefining" the slope as 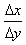 and representing horizontal lines as equations of the form x = k. We go beyond the "answers" and beyond correcting any basic misconceptions that arise. We discuss such issues as what made them believe that the functions were linear. The responses usually begin at a vague level—"The graphs were straight," get pushed to those that use the phrase "constant slope," and then on to those that describe what it means for the slope to be constant. The teacher-led discussion also reviews the fact that vertical lines are not linear functions and the fact that horizontal lines are actually considered constant functions.
and representing horizontal lines as equations of the form x = k. We go beyond the "answers" and beyond correcting any basic misconceptions that arise. We discuss such issues as what made them believe that the functions were linear. The responses usually begin at a vague level—"The graphs were straight," get pushed to those that use the phrase "constant slope," and then on to those that describe what it means for the slope to be constant. The teacher-led discussion also reviews the fact that vertical lines are not linear functions and the fact that horizontal lines are actually considered constant functions.
The reason I love this first day, however, is that next (or perhaps on day two), we look at the same three graphs but with the new assumption that the scale units on each axis are 0.001. Although the questions and comments vary wildly from year to year, the discussion is always lively. I do not give in to their requests to have me "zoom out," but I do eventually tell them that the graphs are those of f (x) = x3+0.002, and h(x) = sin(2x). Their challenge is to identify which is which and to be prepared to give a lucid explanation of their responses. At the end of day one (or two), my students have a remarkably good understanding of the concept of local linearity—just from observing the original graph and then the relationship between the two below:
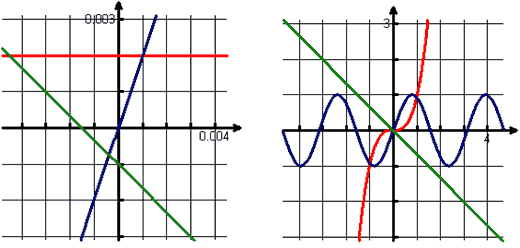
For the next week or two, we
- Create linear functions to model the behavior of nonlinear functions in a neighborhood of x = a (including the fact that we would want our linear model to contain (a,f(a)) and have a slope that would make it appear to behave as y = f (x) does at x = a). We also discuss whether or not there might be a "best" linear model (and eventually arrive at the need for a limiting value, as
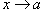 , for).
, for). - Investigate patterns that lead to the concept of the derivative as a function. We do this by assigning each student in the class two or three x-values at which to suggest the slope of a good linear model for a particular function. We plot the collected data and make conjectures about functions that might model this data. For example, after collecting data about slopes of good linear models for f(x) = sin(x), most students are ready to make the conjecture that the cosine function appears to be a good model for our resulting data.
- Define the slope of the best linear model as
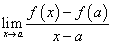 , provided that limit exists.
, provided that limit exists. - Use the definition of the derivative to discover derivative functions for polynomials and other algebraic functions.
This approach is so much more fun and satisfying than beginning with review (much of which is now done in the context of our explorations), and my students find many of the applications of derivatives to be nearly "obvious" with this firm grasp of local linearity. In fact, students see the derivative definition as nothing more than formalizing a concept that seems intuitive. Seeing is not only believing; it is also understanding.
L'Hôpital's Rule
At the end of the Reading for several years, Texas Instruments provided a workshop for Readers to learn how to use technology most effectively in the calculus classroom. At one of the TICAP workshops, Tom Dick was discussing applications of the derivative and showed us a visual "proof" of L'Hôpital's Rule. Although he did not claim that it was a proof, he did suggest that it added considerable insight into why the famous rule works. In fact, if most of us were honest, we would admit that reading through a proof of the theorem is not especially enlightening.
After only a few weeks of the school year, my class and I consider the following picture:
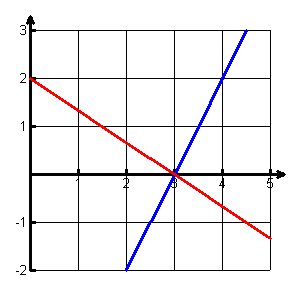
The graphs are those of two linear functions that intersect on the x-axis. We write the rules for each and then form a ratio of the two rules. For the graph above, the two functions are 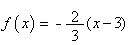 and g(x)=2(x-3). The resulting ratio of becomes
and g(x)=2(x-3). The resulting ratio of becomes 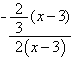 .
.
If 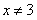
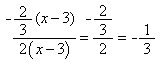 .
.
Suppose we were interested in evaluating 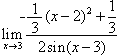 (which is unlikely except in a textbook problem set). We arrive at an indeterminate form of the type we have often discussed when investigating derivatives from the definition. This time, however, there does not appear to be any clever algebra or substitution to make our life simple. In fact, however, the two linear graphs above (f(x) and g(x)) are the tangents to the respective graphs of the numerator (green line) and the denominator (pink line) at x = 3.The numerator and denominator functions of our limit expression are best modeled by those lines, as seen below:
(which is unlikely except in a textbook problem set). We arrive at an indeterminate form of the type we have often discussed when investigating derivatives from the definition. This time, however, there does not appear to be any clever algebra or substitution to make our life simple. In fact, however, the two linear graphs above (f(x) and g(x)) are the tangents to the respective graphs of the numerator (green line) and the denominator (pink line) at x = 3.The numerator and denominator functions of our limit expression are best modeled by those lines, as seen below:
Therefore, it seems that as long as x is "very" close to 3 (but 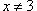 ), we can substitute the nonlinear equations with their tangential linear approximations,
), we can substitute the nonlinear equations with their tangential linear approximations,
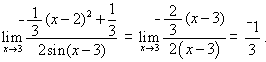
"Wow" is almost always heard, and immediately thereafter, the expected question of whether or not this always "works" arises. We look at a more general case of two linear functions that intersect at (a,0) to discover that 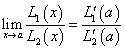 . We acknowledge that we have not proven anything but that all we have previously discussed suggests that if the required conditions exist, L'Hôpital's Rule applies. For some purists, it may not be satisfactory to accept L'Hôpital's Rule based on this development, but my students not only believe it is true but actually understand why the theorem seems to be reasonable. Although L'Hôpital's Rule is not on the AB syllabus, I always address it in an AB class because this highly visual development reinforces the power of local linearity for them.
. We acknowledge that we have not proven anything but that all we have previously discussed suggests that if the required conditions exist, L'Hôpital's Rule applies. For some purists, it may not be satisfactory to accept L'Hôpital's Rule based on this development, but my students not only believe it is true but actually understand why the theorem seems to be reasonable. Although L'Hôpital's Rule is not on the AB syllabus, I always address it in an AB class because this highly visual development reinforces the power of local linearity for them.
The Fundamental Theorem of Calculus
I always approached the Fundamental Theorem from an area perspective. In the early years, I followed up with a development that applied algebraic rules and induction proofs to the applications of Riemann sums associated with simple polynomial functions. Finally, I topped it all off with the telescoping sums proof based on the Mean Value Theorem found in my textbook. I would proudly announce that we had just proved the Fundamental Theorem of Calculus. Unfortunately, my students and I did not understand the Fundamental Theorem at all. In fact, I believed, and taught them to believe, that the Fundamental Theorem basically showed how to evaluate an integral. Oh dear, former students, forgive me!
I sat in on workshop sessions in which one of my mentors, Ray Cannon, approached the concept very differently—from a velocity perspective. I assured him over and over that this was not how students best understand the concept. In fact, I argued with him for three years as I watched him do the same presentation at other workshops, until I had my own "Wow!" moment and was converted. Since then, I've never introduced the Fundamental Theorem using area, and I have many students who should be in Ray's debt as well. The following is a quick overview of my version of this new, and more meaningful, approach.
Several of my students each year are in an AP Physics C class and have learned to associate area under a velocity graph with distance. They are not sure why it "works," but they are good at doing it. Therefore, I begin my class with a random table of positive velocity values and tell them that there is an object moving along a straight line that never decreases in velocity. Then I provide them with a table of data and ask them to provide an estimate of the distance the object moved in the given time period.
| t, seconds | 0 | 2 | 3 | 7 | 10 |
|---|---|---|---|---|---|
| Velocity in meters/second | 8 | 11 | 15 | 23 | 25 |
Without a function rule, most of my physics students are stymied for quite a while. As the groups begin to talk, however, many come up with a reasonable estimation that they can support. Many of the physics students graph the data and use trapezoids. Others find the average of the minimum and maximum rates for each interval and apply d=rt to those values. We discuss all proposed estimates and methods, and often find relationships between methods. However, we ultimately move to looking at the following graph of the data and to finding upper and lower bounds on the distance traveled for this nondecreasing function, using Riemann Sums.
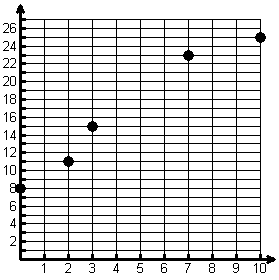
The grid below, for example, shows the lower bound estimation: 8(2)+11(1)+15(4)+23(3)=156 meters
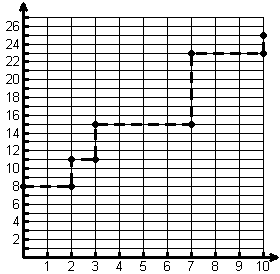
What students "see" is that their old friend d=rt applies because the assumption has been made that the velocity remained constant over each subinterval. We acknowledge that the vertical components are not realistic, but we also acknowledge that this has given us a reasonable lower bound on the distance traveled. Next we find the upper bound by the same approach and look at why the average of the upper and lower bounds will minimize our error. We spend the remainder of the class period investigating what happens as more data is provided for the same ten-second interval. What happens to the upper and lower bounds? How about the error? Why is this happening? By the end of this class period, we have discussed Riemann sums (left, right, and even midpoint), and we have used geometry to support the fact that using trapezoids provides the same result as the average of the left and right hand Riemann Sums approach.
In the next class period, we investigate a nonlinear function on an interval [a,b] using a program we have written for finding Riemann Sums. The function shown below is typical of what I seek as an example because both positive and negative products affect the result.
Students quickly recognize that what they have believed to be a method of estimating distance traveled turns out to be a method for estimating displacement. Students "see" why the result is displacement, however, because they actually watch the sum as it is affected by negative values for v·t that occur when the velocity graph is below the time axis. The class acknowledges that, once again, we seem to be rushing headlong toward a limiting value—this time associated with Riemann Sums. This is now a good opportunity to introduce the integral notation.
Finally, we summarize what we have discovered—the limiting value of our Riemann sums yields the displacement of the moving object over the time interval. In symbols, we write 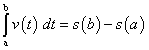 . From here, a simple substitution is all we need:, and—voila!—the Fundamental Theorem. Although I seldom go through the actual proof, my students have a much better understanding of why a definite integral is often described as an accumulator of products involving rates. They find it easier to apply this knowledge to new situations, and they have even stopped asking "Where did the dt go?"
. From here, a simple substitution is all we need:, and—voila!—the Fundamental Theorem. Although I seldom go through the actual proof, my students have a much better understanding of why a definite integral is often described as an accumulator of products involving rates. They find it easier to apply this knowledge to new situations, and they have even stopped asking "Where did the dt go?"
Conclusion
I chose these three examples for two reasons. First, they define three of the many insights I have gained as a direct result of being involved with the remarkable folks I have met along the way in the AP Program. Second, they dramatically illustrate how I have grown as a teacher—finding ways to help my students maximize their level of understanding and minimize the pain and confusion that I used to cause them by trying to provide a proof of every major theorem and make them work through pages of procedural drill. Do I value proof? Yes! Do I believe that skills are still important in the life of the practitioner? Yes! Do I still follow up with some of the more accessible proofs and expect students to be competent with fundamental procedures? Yes! Do I believe that it is in doing the proof or in doing pages of problems that my students gain understanding of and appreciation for the power of the theorems and concepts? No! In fact, I now have more students who decide to major or minor in mathematics than I have ever had before. Most want to take additional mathematics courses in college, and most who did fared well.
I would still be mired in training students to develop skills and procedures—and believing that proof was what led to understanding—if I had not had many good mentors in the AP Program. They have helped me discover not only the wonder and power of calculus but have also affected the way I approach all my classes, from Algebra I through AP Calculus. To all of them—thanks!
This article was presented as a lecture during Professional Night at the June 6, 2004, AP Calculus Reading.
J. T. Sutcliffe holds the Founders Master Teaching Chair at St. Mark's School of Texas in Dallas. A recipient of the Presidential Award for mathematics teaching, as well as Siemens and Tandy Technology Scholars awards, she has served as a member of the AP Calculus Development Committee and as an AP Calculus Table Leader and Exam Leader. In addition, J. T. has served on advisory and developmental boards for the College Board Vertical Team and Building Success committees and has also helped develop Pacesetter: Mathematics with Meaning, a teacher professional development project for the College Board.
Authored by
- J. T. Sutcliffe
St. Mark's School
Dallas, Texas