Residue of Calculus: Learning That Lasts
When I began thinking about writing this article, I considered several themes. One was how calculus ideas occur in everyday life, mostly undetected and, if noticed, rarely connected to calculus. I currently teach a course I developed entitled Mathematical Reasoning in a Quantitative World, in which the mathematical and statistical reasoning comes from analyzing recent newspaper and magazine articles. One of those articles is from the New York Times and includes the following graphic.
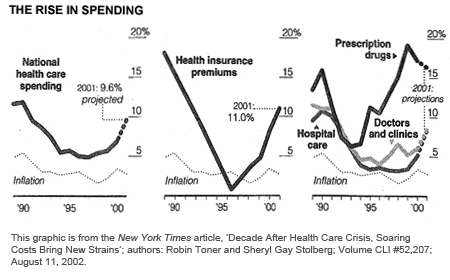
When we discuss this article in class, I ask my students several questions. First, why are these graphs entitled "The Rise in Spending"? We struggle with that for a bit, and then we decide that these are not graphs of spending but rather graphs of the change in spending, more specifically the change per year in spending. The center graph is a good illustration. (Why?) I ask the students to use the information in this graph, assume that the cost of health insurance premiums was $5 billion in 1989, and graph the cost over the next 10 years. In spite of the fact that there are only 10 to 12 discrete data points, we often do as the Times did and draw line segments through the data points. (Note that AP® Exam questions about discrete data often state the assumption that there is a differentiable function whose graph includes the given data points.) I suggest to the students that we construct a "line" graph, which is reasonable since costs likely did increase incrementally over the course of each year. If we do that, the graph over [1990, 1996] has an identifiable shape, as does the graph over [1996, 2001]. What are those shapes? Of course, using a calculus concept, you can determine that this graph of the "first derivative" is decreasing over the first interval and increasing over the next. Therefore, the graph of spending should be concave downward and then concave upward. Even the students in my class who have had calculus (in high school) do not make this connection, and, I should add, I do not expect that students who have had our calculus course(s) at the university to make the connection either.
Now as I have suggested, we get a reasonable representation of the change in costs by assuming they change according to a differentiable function. (Actually, we are using discrete values of the rate of change, values of the rate of change from one year to the next.) We are not going to take a derivative; we are actually integrating, and as we all know, we can integrate functions that are not differentiable. Therefore we are not worried about the nondifferentiability of the rate of change function in 1996. We are assuming that the rate of change of spending behaves like the Times has indicated that it does (nicely piecewise linear), and we investigate what that means about the graph of the spending function. Knowing that concavity is a measure of the monotonic behavior of the derivative allows us to better understand and verify our graph. No calculus methods are involved, rather calculus ideas, which brings me to this article's theme.
Residue of Calculus
What follows are some of my ideas about what is important in calculus, focusing on the content of the AP Calculus AB and BC courses. My ideas are strongly influenced by what I think people remember about calculus and what applies to reasoning in the world beyond school and college. My conclusions apply more strongly to the calculus student who does not continue in the physical sciences, engineering, or mathematics and does not practice the methods of calculus beyond the two or three college courses. By the way, the latter group of students has been growing in recent years and probably constitutes most students who study calculus in high school or college.
As other calculus teachers have observed, one criterion for what is important in a college course is what one remembers in 15 years. Of course, we calculus teachers and most of our students act as if we believe that what is important is what students remember for the final examination or the AP Exam. Research on learning and our experiences tell us that these ideas are likely different.
I chose the title "Residue of Calculus: Learning That Lasts" to suggest what remains usable after many years in a student's memory of calculus. And what is that? I am quite sure it is different for each individual. We teachers are not a very good test case, because most of us have stayed close to calculus over the years since our AB and BC courses or their counterparts in college. Instead, I am relying on two sources to support my analysis of what remains usable. The first source is what I remember without any refreshing when I have been away from calculus for a few semesters. The second source is results from learning research on recall and transfer. I will not try to detail the research results I am relying on or even whether I am guessing based on my experience. Even though the latter is very influential, I hope that what I say makes enough sense to be plausible.
Results from Learning Research
A National Research Council committee (2000) gleaned the following three principles from recent research on learning:
- Students come to the classroom with preconceptions about how the world works. If their initial understanding is not engaged, they may fail to grasp the new concepts and information that are taught, or they may learn them for the purposes of the test but revert to their preconceptions outside the classroom.
- To develop competence in an area of inquiry, students must (a) have a deep foundation of factual knowledge, (b) understand facts and ideas in the context of the factual framework, and (c) organize knowledge in ways that facilitate retrieval and application.
- A "metacognitive" approach to instruction can help students learn to take control of their own learning by defining learning goals and monitoring their progress in achieving them.
While I believe all three of the above should inform how we teach calculus, the second statement is my primary focus in this article. Pictures are great factual frameworks for me, and, I believe, for most people. Some 15 years ago, as the new member of the AP Calculus Development Committee, I had to give the "math talk" at the annual committee workshop. I think I called my talk the "Calculus Coloring Book"—and later "Pictures of Calculus"—and I have given roughly the same talk a few times since. Here are two examples from that talk, without the transparency overlays that made it interactive.
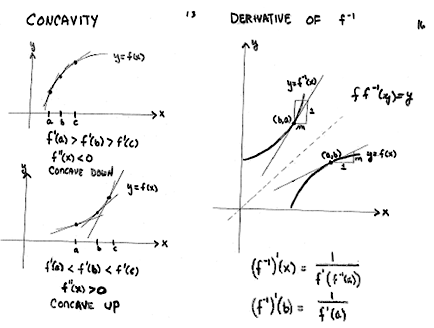
In the discussion below of the Fundamental Theorem of Calculus, there are two graphics that I believe help greatly to sort out what this theorem means.
One theory that has influenced my approach to helping students learn is the Dreyfus model of human learning as described by Flyvbjerg (2001). This model operates with five levels of performance: novice, advanced beginner, competent performer, advanced performer, and expert. The theory notes many differences between novices and experts, but a few stand out to me. Novices follow rules independent of context; experts act spontaneously from intuition seemingly based on experience and without analytic deliberations. Most of us have experienced being a novice—for example, learning to drive an automobile and following various rules about getting the car started, changing gears, stopping, and even steering the vehicle. In contrast, many of us now drive automobiles without conscious deliberations about when and how to perform various actions. Certainly we have moved up the Dreyfus levels toward expert status in this one performance.
Another difference between novices and experts is that novices process information and rules discretely while experts batch information. In fact, as people move from novice to expert, they replace rules-based actions with holistic recognition of situations. Although most students will not become experts in calculus or any part of mathematics, I believe the model of progression in performance is helpful to the teacher. For example, the pictures above are batches of information I carry around. When concavity is the issue, I use the picture on the left as a factual framework. The fact that these factual frameworks are different for different individuals is intimately tied to the metacognition principle above. Furthermore, our students may have their own factual frameworks for calculus concepts, and we need to understand those, if possible, before we begin imposing our own framework on them—that is, we need to keep the first principle in mind. I could continue to explore these principles and the Dreyfus model as they apply to teaching calculus; however, I want to focus more on the calculus than on the results of learning research.
The Nature of Calculus
Calculus is a rich, extensive, and coherent body of knowledge. Tom Apostol introduced volume 1 of his Calculus book in 1961 with these words.
Calculus is more than a technical tool—it is a collection of fascinating and exciting ideas that have interested thinking men for centuries. The ideas have to do with speed, area, volume, rate of growth, continuity, tangent line, and other concepts from a variety of fields. Calculus makes us stop and think carefully about the meaning of these concepts. Another remarkable feature of the subject is its unifying power. Most of the ideas can be formulated so that they revolve around two rather specialized problems of a geometric nature.
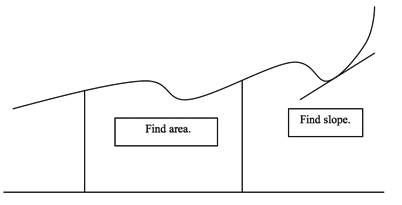
The two problems (illustrated below) that Apostol goes on to describe are (1) assigning a number that measures the area of the region under a graph of a function and (2) assigning a number that measures the steepness of a line tangent to the graph of a function. Of course, to solve either problem, Apostol defines the notion of a limit and uses that to define the concept.
Solving both these problems and developing the idea of limit, derivative, and integral is not the end of the story. Some 2,500 years ago, the Greeks formulated the notion of the integral—that is, finding areas of regions. Archimedes (287-212 BCE) used the method of exhaustion to find the formula for the area of a circle and other special figures. About 1,800 years later, in the sixteenth century, the adoption of Hindu-Arabic numerals in Western Europe and the development of algebraic notation set the stage for the groundbreaking work of Newton and Leibniz in the seventeenth century. It was the recognition of the connection between the derivative and the integral, namely the Fundamental Theorem of Calculus (FTOC), that gave credit for the formulation of calculus to Newton and Leibniz. That should signal the importance of the FTOC, which I address more fully below.
Learning Goals of Calculus
How often do you review the learning goals for AP Calculus? Before 1998, we had no articulated learning goals. While preparing the new AP® Calculus Course Description, the AP Calculus Development Committee formulated nine learning goals. The following list shows key words from those goals:
- Representations and connections
- Rate of change and linear approximation
- Accumulation
- Fundamental theorem
- Communication
- Model using differential equation or integral
- Using technology to solve, experiment, interpret, and verify
- Reasonableness of solutions
- Appreciation
These key words, mostly concepts or processes, reflect what I believe to be important in calculus and what I believe can be retained and used over the years. Notice that the methods of calculus—methods of differentiation and antidifferentiation—are not prominent among these learning goals.
Did I understand this as the core of calculus when I took Calculus I and Calculus II at Western Kentucky University under Hugh Johnson in 1959-60? Of course not. Although Mr. Johnson was an excellent teacher, I reached my current beliefs about calculus only after years of reflection and study. Knowing what should be taught does not ensure that it can be taught or that one is able to teach it.
In fact, my student work in calculus courses focused very much on methods, more so than today's courses. Our text was by Granville, Smith, and Longley (1957), which was a revision of editions dating from 1904. Notable were two chapters: (1) "Formal Integration by Various Devices" and (2) "Reduction Formulas: Use of Table of Integrals." We covered both chapters and had an hour-long examination with four problems over reduction formulas. A typical homework assignment on reduction formulas was to verify several statements like the following:
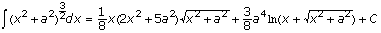
Do I remember how to do this? No. Do I remember any of the reduction formulas? No. I might be able to derive some of them on antiderivatives of products of powers of trigonometric functions. Even doing the above by taking a derivative is a bit of work. I did learn discipline, organization, and care in my work from Mr. Johnson's classes. That discipline and organization seems to be weaker among today's calculus students, and from my experience with the AP Examination, it has worsened with the introduction of calculators.
In class, I recall that Mr. Johnson derived all eight reduction formulas in the textbook. The various devices for formal integration included integration by parts, partial fractions, and substitution. Every formal integration problem was a puzzle, and solving the puzzle often required ingenuity and false starts. Nevertheless, we learned problem solving and reasoning. Very often, though, the results were neither memorable nor applicable, somewhat like the result of solving a sudoku puzzle.
The reduction formulas and somewhat mysterious substitutions are only a part of what I have forgotten about calculus. I cannot remember the form of integrals that yield to multiple uses of parts, and I do not remember how to use polar, cylindrical, and spherical coordinates. I would have to work quite a bit to recover the polar equations of conics. I think I could use cylindrical shells because that is just an example of an accumulation situation. That, to me, is the key. We should remember general methods and concepts and let them guide us to more specialized methods.
Solving a calculus problem should have value beyond the answer. Constructivists believe that lectures cannot deliver understanding. A student should develop understanding by working through examples and concept maps. I subscribe to that theory and believe we should avoid memorization and mimicry exercises, which may have value beyond the answer but probably not beyond the course and most likely not beyond school.
My View of Calculus
Calculus has threads that run throughout and beyond—rate of change, accumulation, approximation, applications, and differential equations. I believe it promotes formulation of factual frameworks to note when your subject matter follows these threads. Along with the processes of connecting, number sense, communication, representation, and technology, these threads give a concept map that can be helpful to keep in mind as courses unfold. The following diagram shows one way of conceptualizing calculus, and I believe that such a conceptualization is important -- seeing the big picture. Just when, if ever, we should give such suggestions to students is not clear to me, but I believe we should encourage students to develop their own reasonable conceptualization.
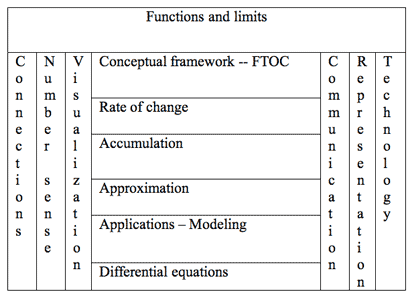
Important Theorems and Concepts
The FTOC is clearly important, and I discuss it in some detail below. So, aside from the FTOC, what else is important? To help students understand derivatives and integrals and to utilize their power, we develop several key concepts, described below. Unfortunately, many of these concepts do not play key roles in many calculus courses, so their importance is lost on the students. I believe that is a mistake, one that I have made many times.
Mean Value Theorems
There are two, one for derivatives and one for integrals. I remember quite a long discussion among members of the AP Calculus Development Committee about whether or not the Mean Value Theorem (MVT) for derivatives should be a part of the Course Description. In retrospect, I am very pleased that the MVT survived.
MVT for derivatives: If f is continuous on [a, b] and differentiable on (a, b), then there exists a number c, a ‹ c ‹ b, such that
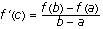
Now, I have used the standard letters for the endpoints of the integral and the guaranteed value in the interval. These are so standard that some students and faculty classify MVT exercises (not problems) by "find c." This is an example of information that students should not recall. That is, they should remember the MVT differently.
As examples of what I am saying, consider the following information that is written in the memories of legions of students. No doubt you will recognize the concepts behind these cryptic but ubiquitous expressions.
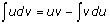 |
, or is it | 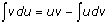 |
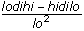
FOIL
HOMES
The final one above might be useful since there is no logical method (as far as I know) to memorizing the names of the Great Lakes. Unfortunately, many students feel that same way about the Pythagorean theorem, area of a trapezoid, integration by parts, quotient rule, and product of two binomials.
Let me suggest other ways to state the MVT.
MVT for derivatives: If f is continuous on [a, b] and differentiable on (a, b), then there exists a number between a and b where the instantaneous rate of change of f is equal to the average rate of change of f over [a, b].
Or, even better:
MVT for derivatives: If a function is continuous on a closed interval and differentiable on the interior of that interval, then there is a point in the interval at which the instantaneous rate of change of the function is equal to the average rate of change of the function on the closed interval.
After all, this is called the Mean Value Theorem, and the reason for that designation is hidden in the first statement. The Mean Value Theorem is a special case of Cauchy's theorem. The proof of Cauchy's theorem is similar to the proof of the MVT, and it is useful when you investigate the geometry of curves defined parametrically.
One can argue the virtue of brevity, but too often, brevity begets reduced understanding. Besides, students need to develop the ability to state mathematical results using normal English words and sentences. In addition to developing better communication skills, this reduces the inclination for students to believe that math class is different in all respects from their other classes.
MVT for integrals (Average Value Theorem): If f is continuous on [a, b], then there exists a value c in [a, b] so that
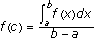
Another way of saying this is that there is a point in a closed interval at which a function assumes its average value. This assumes that one recognizes the integral of the function over the interval divided by the length of the interval as the average value of the function.
Pythagorean theorem: The square of the hypotenuse of a right triangle is equal to the sum of the squares of the other two sides.
Here, of course, we mean the squares of the measures of the sides and hypotenuse, and we should say that early on and then utilize the briefer version.
Area of a trapezoid: The area of a trapezoid is the product of the average of the lengths of the two parallel sides and the distance between them.
Integration by parts: Of course, what you should remember if you ever need the parts method is the fundamental relationship d(uv) = udv + vdu.
Other conceptually important results include the chain rule, product rule, and Intermediate Value Theorems.
The chain rule is an important concept because it shows how to compute rates of change of compositions. This gives rise to a technique of antidifferentiation referred to as substitution.
The product rule is an important concept because it shows how rates of change are affected by products of functions, and it gives rise to integration by parts.
Both the Intermediate Value Theorem (IVT) for continuous functions and the IVT for derivatives are stated below in the my discussion of the FTOC. The IVT for continuous functions has many applications about existence. The IVT for derivatives is not well known to calculus students, but it tells you something about the nature of functions that are derivatives, which is explored below. The IVTs are existence results: they do not tell you how to find the solution. The two-pancake problem is a good example.
Two-pancake theorem: For any two pancakes in a plane, there is a single knife cut that simultaneously bisects both pancakes (as below).
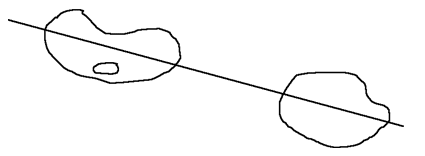
Applications to Remember
The applications of calculus are wide-ranging, and some of them cluster around ideas that promote batching. I will not explore applications here, but I believe the following clusterings are helpful and have value beyond the course for all students.
- Optimization—Maxima and minima
- Qualitative analysis of graphs—Monotonicity, shape, end behavior
- Area and volume—Accumulations
- Approximations—Series, numerical methods
- Work, centroids, force, and pressure—Also accumulations
The Fundamental Theorem
The Fundamental Theorem of Calculus is indeed fundamental,1 much more so in my view than the other two fundamental theorems in undergraduate mathematics: Fundamental Theorem of Arithmetic and Fundamental Theorem of Algebra.
We often state the FTOC as two theorems, called either first and second or parts 1 and 2. Sometimes we present one of the two as a corollary of the other.
FTOC 1: If f is a continuous real-valued function on the interval [a,b] and 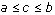 , then the function defined by
, then the function defined by  has a derivative at any x in (a,b), and
has a derivative at any x in (a,b), and 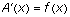 .
.
FTOC 2: If f is a continuous real-valued function on the interval [a,b], c and d are in the interval [a,b], and A is any antiderivative of f, then 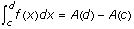 .
.
Here's another way of expressing the FTOC (Johnson and Kiokemeister 1960).
FTOC: If f is a function continuous in a closed interval, then:
- The function f has antiderivatives in this interval.
- If F is any antiderivative of f, and a and b are numbers in the given interval,
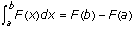
f ' (b) .
Proof: Put 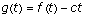 for
for 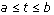 .
.
Then,
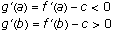
Let  be a point at which g attains its minimum. Then show that g does not attain its minimum at either a or b using the fact that
be a point at which g attains its minimum. Then show that g does not attain its minimum at either a or b using the fact that 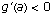 and g ' (b) > 0, and these are limits of
and g ' (b) > 0, and these are limits of 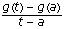 and
and 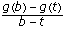 . Hence
. Hence 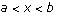 . Now using the fact that the derivative of a function where it attains its minimum is 0, we have g ' (x) = f ' (x) - c = 0 or f ' (x) = c.
. Now using the fact that the derivative of a function where it attains its minimum is 0, we have g ' (x) = f ' (x) - c = 0 or f ' (x) = c.
Corollary (Intermediate Value Theorem for continuous functions): If f is continuous of [a,b] and 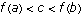 , then there is x,
, then there is x, 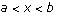 , so that f(x) = c.
, so that f(x) = c.
Proof: Use the FTOC and the IVT for derivatives. (This argument assumes that you do not use the IVT for continuous functions to prove the MVT for integrals and then use the MVT for integrals to prove the FTOC.)
Corollary: Functions that are derivatives cannot have simple discontinuities.
Recall: The function f has a simple discontinuity at a point c, provided f is discontinuous at c while both 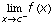 and
and 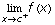 exist. Examples are removable discontinuities and jump discontinuities.
exist. Examples are removable discontinuities and jump discontinuities.
Hence an example of a function that is not a derivative (question 2) is a simple function such as
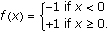
This result (IVT for derivatives) made answering question 2 easy but indicates that answering question 3 requires some work. Still, we can do it.
Example 1.
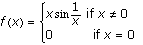
If 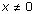 , then
, then 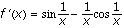 . If x = 0, then
. If x = 0, then 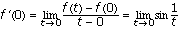 , which does not exist.
, which does not exist.
Example 2.
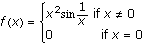
For 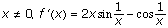 using the definition of the derivative,
using the definition of the derivative, 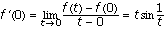 . Since
. Since 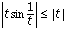 , we have f'(0) = 0.
, we have f'(0) = 0.
Now, f is differentiable at all points x, but f' is not continuous at 0 since 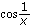 does not have a limit at 0.
does not have a limit at 0.
FTOC on the AP Exam
Most occurrences of the FTOC on past AP Exams fit into one of the following categories.
-
Evaluation of definite integrals—These are commonplace, but sometimes students might see the problem stated as follows: Use the FTOC to evaluate this definite integral. That means the student should use an antiderivative instead of a numerical process on a calculator.
-
Problems with functions defined by integrals&mdashThese are of two basic types:
-
Given f, define the function g by
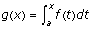 . Investigate g.
. Investigate g. -
Given f' and a value
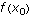 , find f.
, find f.
This second type (b) is worth mention because it prompts another statement of the FTOC. We are looking for f, knowing the derivative of f. So we are looking for an antiderivative of f'. Since
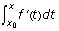 is an antiderivative of f', we know that
is an antiderivative of f', we know that 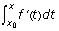 and f differ by a constant, or
and f differ by a constant, or 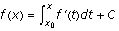 . Evaluating at gives
. Evaluating at gives 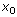 gives
gives 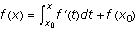 .
.Why We Teach and Test Methods
The methods of calculus are easiest to teach, and teaching them matches the students' expectations of mathematics classes. I believe two features dominate those expectations:
- Mathematics is not relevant to students' everyday lives.
- Mathematics classes proceed with the instructor demonstrating template problems and methods and assigning some exercises that more or less follow the template.
Questions that evaluate conceptual understanding are less adaptable to this template exercise process, and they are more difficult to write and to score. Teachers who have participated in the AP Calculus Reading for several years can probably remember free-response questions with scoring guidelines that more or less went like this: "3—Looks okay, 3—Okay here too, and 3—Here too." For example, the following is the total right-hand column for an area and volume question in 2005—fairly typical of scoring guidelines for this type of item.

Compare that with the guidelines for 1998 AB2/BC2 or 2005 AB4. Questions asking to apply a method that is well practiced and somewhat routine are likely to have fairly uniform responses and we can score them quickly. More complex questions generate responses that require slower reading—that is, if there are not large numbers of blank responses.
In my mathematical reasoning course, we rarely see two situations that are the same. Students often lament, "We have not seen that kind before," and "What's the formula?" We have trained them well—rather not so well.
I am pleased with what I see on recent AP free-response questions, but I know how much more effort it takes to write and score those questions. Nonetheless, many of them are getting at the concepts of calculus rather than the methods.
That is the learning that lasts, and that's critical. However, we are swimming upstream on this. High-stakes testing is driving much of the instruction and learning in K-12 mathematics, and many of the questions on high-stakes tests are template questions. If high-stakes testing continues like this, students will have even stronger expectations of template problems and methods-based questions. That will make your job more difficult and probably less pleasant.
Let's keep swimming.
Notes
1. Webster's Dictionary defines fundamental as an adjective as basic, essential, and original and as a noun as a primary principle.
References
Apostol, T. A. 1961. Calculus. Vol. 1. Waltham, Massachusetts: Blaisdell Publishing Company.
Flyvbjerg, B. 2001. Making Social Science Matter. Cambridge, UK: Cambridge University Press.
Granville, W. A., P. F. Smith, and W. R. Longley. 1957. Elements of the Differential and Integral Calculus. Boston: Ginn and Company.
Halpern, D., and M. Hakel. July/August 2003. "Applying the Science of Learning to the University and Beyond." Change.
Johnson, R. E., and F. L. Kiokemeister. 1960. Calculus with Analytic Geometry. Boston: Allyn and Bacon.
National Research Council. 2000. How People Learn: Brain, Mind, Experience, and School. Expanded ed. Washington, D.C.: National Academies Press.
-
Authored by
Bernard L. Madison
University of Arkansas
Fayetteville, Arkansas