Frozen in Time
Consider the following questions:
-
Let
 for 0 ≤ t ≤ 30. Is F increasing or decreasing at t = 7?
for 0 ≤ t ≤ 30. Is F increasing or decreasing at t = 7? -
Let
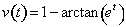 for t ≥ 0 be a particle's velocity at time t. Is the speed of the particle increasing or decreasing at t = 2?
for t ≥ 0 be a particle's velocity at time t. Is the speed of the particle increasing or decreasing at t = 2? -
If
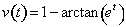 for t ≥ 0 is the velocity of a particle moving along the y-axis, and the particle is at y = -1 when t = 0, is the particle moving toward the origin or away from the origin at time t = 2?
for t ≥ 0 is the velocity of a particle moving along the y-axis, and the particle is at y = -1 when t = 0, is the particle moving toward the origin or away from the origin at time t = 2?
These three questions were on the free-response section of the AP Calculus AB Exam in 2004. The purpose of this article is to indicate that the typical responses to these questions only have meaning in the context of the situation.
Here are the typical responses, which are accepted as correct in the scoring of the AP Exam:
-
Since
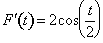 and
and 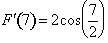 < 0, F is decreasing at t = 7.
< 0, F is decreasing at t = 7. -
Since
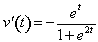 ,
, 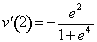 < 0, and v(2)
< 0, and v(2) 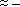 .436278331, the speed of the particle is increasing, since v(2) and v`(2) have the same sign.
.436278331, the speed of the particle is increasing, since v(2) and v`(2) have the same sign. -
In question (2) we observed that v(2) was negative. We also note that the particle's position at t = 2 is given by
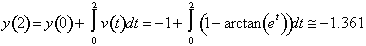 . Thus the particle is moving away from the origin.
. Thus the particle is moving away from the origin.
Now consider a similar question:
-
Let
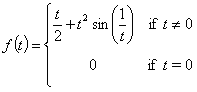 . Is f increasing or decreasing at t = 0?
. Is f increasing or decreasing at t = 0?
Response: Since
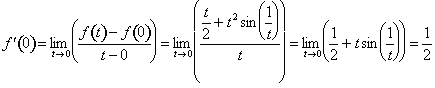 , this would indicate that f is increasing at t = 0. However, let's examine this function a little more closely. We have noted that f´(0) = 1/2. If t
, this would indicate that f is increasing at t = 0. However, let's examine this function a little more closely. We have noted that f´(0) = 1/2. If t  0, then
0, then 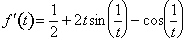 . The graph of f´ near 0 is given below.
. The graph of f´ near 0 is given below.
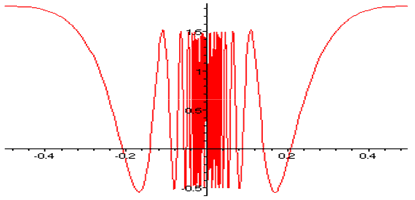
This graph indicates that f´ takes on both positive and negative values in any interval containing 0. This can also be observed analytically by noting that cos(1/t) varies between -1 and 1 in any interval containing 0, and that 2tsin(1/t) approaches 0 as t approaches 0. Hence f´(t) varies approximately between -1/2 and 3/2 near t = 0. This implies that in any interval containing 0, f has subintervals on which it is increasing, and f has subintervals on which it is decreasing. Thus, what is f doing at t = 0? Can you say f is increasing at = 0?
This example highlights the fact that the notion of increasing/decreasing pertains to intervals rather than points. Graphs of the earlier piecewise-defined function f are not really helpful in terms of analyzing the behavior of f near 0. The TI-83 Plus produces some of the following graphs.
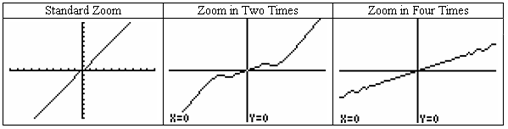
These graphs are not capable of detecting where f is increasing or decreasing. The middle graph above gives some hint of what is happening, but by the time we zoom in four times, we only see that f appears to be increasing near t = 0. By choosing intervals appropriately, we can see places where f is decreasing. The graph on the left below was produced by the TI-83 Plus with the window set as indicated. This indicates an interval, near 0, over which the function f is decreasing. The graph on the right below was produced by Maple®, over an interval even nearer to 0.
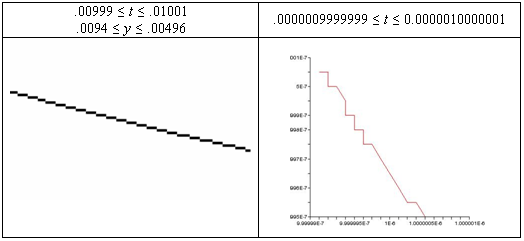
The graph on the right does not adequately (or accurately) represent the function f. A table of values produced by Maple® does give a little more insight and accuracy.
| t | f(t) |
|---|---|
| .0000009999999 | .00000049999969527 |
| .00000099999992 | .00000049999968599 |
| .00000099999994 | .00000049999967681 |
| .00000099999996 | .00000049999966775 |
| .00000099999998 | .00000049999965881 |
| .00000100000000 | .00000049999965001 |
| .00000100000002 | .00000049999964134 |
| .00000100000004 | .00000049999963283 |
| .00000100000006 | .00000049999962446 |
| .00000100000008 | .00000049999961627 |
| .00000100000010 | .00000049999960824 |
In the problems given on the AP Calculus Exam, the behavior exhibited above is not a problem. The functions given there are "nice" in the sense that their derivatives are continuous. Thus if the derivative in those problems was positive at a point, then it would be positive in some interval about that point, hence the function would be increasing in that interval.
I don't know of any movement in the "real world" that results in a discontinuous velocity function. Therefore, the questions asked on the AP Exam make sense in terms of our experience. Those questions all involve a continuous derivative (velocity). Such a derivative, if positive at a point will be positive in an interval about that point, and hence the function will be increasing on an interval containing that point. The "bizarre" function given in problem 4) indicate that the derivative being positive at a point need not imply that the function is increasing on an interval containing that point. Some calculus texts, such as Ostebee and Zorn, define increasing at a point to mean increasing on an interval about that point. With this definition, the AP Exam questions make perfect sense. However, we shouldn't forget that the concept of increasing is an interval concept.
So what direction is a particle moving at t = a? Think of taking a picture of that particle at that time. Can the picture tell you which direction the particle is moving? My answer is that at t = a, the particle is not moving at all. It is "frozen in time."
Jim Hartman teaches at the College of Wooster in Wooster, Ohio. He has been involved with AP Calculus since 1991 as a Table Leader at the AP Reading and through workshops and AP Summer Institutes.
Authored by
Jim Hartman
College of Wooster
Wooster, Ohio