Calculus at the Battle of Trafalgar
Calculating a Strategy
The summer of 2015 marked the 210th anniversary of the British naval victory over a combined French and Spanish fleet in the waters off Cape Trafalgar. During the Napoleonic wars, naval warfare followed certain rules that seem rather formal to us today. The ships in each fleet lined up in a row, sailing parallel to their opponents and firing as they sailed past each other (Figure 1). They repeated this maneuver until one fleet disabled or sank the other. This is known as the directed fire model or conventional combat model.
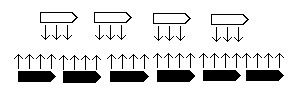
Figure: The White Fleet takes a beating. Image courtesy of the author.
In such an engagement, the fleet with superior firepower will inevitably win. To represent this battle, we begin with a system of differential equations that models the interaction of two fleets in combat. Suppose we have two opposing forces, fleet A with 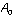 ships and fleet B with
ships and fleet B with 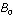 ships initially, and
ships initially, and 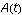 and
and 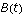 ships at t units of time after the battle is engaged. Given the style of combat at the time of Trafalgar, the losses for each fleet will be proportional to the effective firepower of the opposing fleet. That is,
ships at t units of time after the battle is engaged. Given the style of combat at the time of Trafalgar, the losses for each fleet will be proportional to the effective firepower of the opposing fleet. That is, 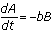 and
and 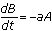 where a and b are positive constants that measure the effectiveness of the ship's cannonry and personnel, and A and B are both functions of time. These equations indicate that the rate at which one navy loses ships depends on only two things: the number of ships in the opposing fleet and the effectiveness of the opposition fire. Assume that the effectiveness does not change throughout the battle so that the rate at which a navy loses ships is proportional to the number of ships in the opposing fleet.
where a and b are positive constants that measure the effectiveness of the ship's cannonry and personnel, and A and B are both functions of time. These equations indicate that the rate at which one navy loses ships depends on only two things: the number of ships in the opposing fleet and the effectiveness of the opposition fire. Assume that the effectiveness does not change throughout the battle so that the rate at which a navy loses ships is proportional to the number of ships in the opposing fleet.
The Questions for Battle
-
Assume that
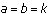 (the two fleets are equal in battle), and show that the total number of ships still fighting is decreasing exponentially by considering
(the two fleets are equal in battle), and show that the total number of ships still fighting is decreasing exponentially by considering 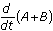 .
. -
Assume that
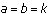 , and show that the difference in the size of the two fleets is increasing exponentially by considering
, and show that the difference in the size of the two fleets is increasing exponentially by considering 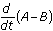 .
. -
Use the results from questions (1) and (2) to solve for A and B as functions of time.
-
If
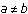 , you can't use the techniques in questions (1) and (2) to determine the number of ships in each fleet as a function of time. If
, you can't use the techniques in questions (1) and (2) to determine the number of ships in each fleet as a function of time. If 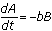 and
and 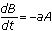 , find
, find 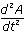 , substitute, and solve for
, substitute, and solve for 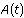 . You will have two solutions to the second-order differential equation. The general solution will be the sum of these solutions. Use this solution to find
. You will have two solutions to the second-order differential equation. The general solution will be the sum of these solutions. Use this solution to find 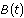 . Ensure that the solutions to question (3) are special cases of this more general solution.
. Ensure that the solutions to question (3) are special cases of this more general solution. -
If
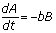 and
and 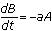 , find
, find 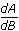 and solve for A in terms of B. This equation will give you the expected number of ships remaining in fleet A when
and solve for A in terms of B. This equation will give you the expected number of ships remaining in fleet A when 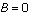 .
. -
The commander of the British fleet was Admiral Nelson. In the now famous Battle of Trafalgar, he exhibited cunning military strategy. In one account of the battle, Nelson expected to have 27 ships in the British fleet (B) and predicted that the French/Spanish Armada (A) would have 34 ships. In planning his strategy, Nelson believed that the British fleet was better prepared (and better led) than the French/Spanish Armada. Suppose that
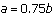 .
.If Nelson's 27 ships fought a conventional battle against the 34 ships in the French/Spanish Armada with
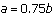 , would he win? How many ships would remain in the winning fleet?
, would he win? How many ships would remain in the winning fleet? -
Instead of sailing parallel to the French/Spanish fleet, Nelson planned to sail through the middle of the fleet, cutting it in half and fighting two separate conventional battles. In one battle, he would have numerical superiority and consequently win that battle. In the other, he would have fewer ships and lose. But, with the ships that remained in the battle that he had won, would he be able to defeat the ships remaining in the French/Spanish fleet in the battle that they won? In a third and decisive battle, the British fleet would be victorious. Note that Nelson assigned himself the task of leading the portion of his fleet expected to lose its battle.
Show, using the results from question (5), how Nelson could arrange his 27 ships to defeat a larger fleet of 34 ships using a three-battle plan as described above with
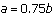 . According to our model, how many ships would we expect to survive the final battle?
. According to our model, how many ships would we expect to survive the final battle?
Solutions
Answer the questions in full before viewing the Solutions and Commentary.
-
Assuming the combat effectiveness of the combatants is equal, when we add the two equations together, we get
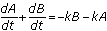 . Recall that the sum of derivatives is the derivative of a sum. So we actually have
. Recall that the sum of derivatives is the derivative of a sum. So we actually have 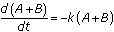 .
.This equation is a variation of the basic differential equation for exponential functions
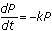 , where
, where 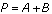 . The solution to
. The solution to 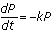 is
is 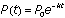 , and so the solution to our equation is
, and so the solution to our equation is 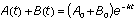
This means that the total number of ships in the battle decreases exponentially over the time of the battle.
-
In a similar manner, we can consider the difference in the two defining differential equations.
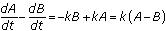 is equivalent to
is equivalent to 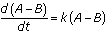 and so
and so 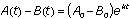
In the course of the battle, the difference in the number of ships that remain in the winning fleet A and those remaining in the losing fleet B increases exponentially.
-
We now have two equations in two unknowns, A and B. Solve for A by adding the two equations from questions (1) and (2) together to eliminate B. This yields
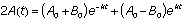 and
and 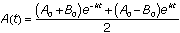 . Solving for B, we find that
. Solving for B, we find that 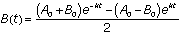 .
. -
If
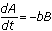 and
and 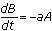 , then
, then 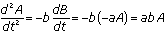 . This shows that the second derivative of A is proportional to A. What function is this? Only the exponential function has this property. However, there are two solutions, since the exponent could be either positive or negative. Both
. This shows that the second derivative of A is proportional to A. What function is this? Only the exponential function has this property. However, there are two solutions, since the exponent could be either positive or negative. Both 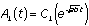 and
and 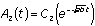 satisfy the differential equation
satisfy the differential equation 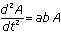 . The general solution, then, is the sum of the two.
. The general solution, then, is the sum of the two. 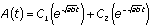 is the general solution to the second-order differential equation
is the general solution to the second-order differential equation 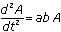 .
.Now,
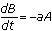 . This means that
. This means that 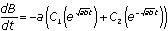 . By integration, we find that
. By integration, we find that 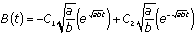 . Since we have
. Since we have 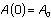 and
and 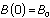 , we can solve for
, we can solve for 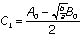 and
and 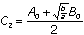 . Notice that if
. Notice that if 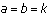 , we have the same solutions as in question (3).
, we have the same solutions as in question (3). -
We know that
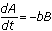 and
and 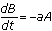 . So, from the chain rule and inverse function rule, we have
. So, from the chain rule and inverse function rule, we have 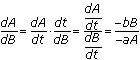 and
and 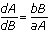 . This is a separable equation, so
. This is a separable equation, so 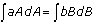 , and it follows that
, and it follows that 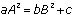 .
.The initial conditions give us
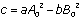 , so
, so 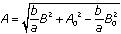 . The end of the battle occurs when
. The end of the battle occurs when 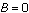 . Substituting into the equation above, we find that the number of ships in fleet A at the end of the battle is
. Substituting into the equation above, we find that the number of ships in fleet A at the end of the battle is 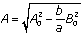 .
.If fleet B wins, then the expected number of surviving vessels is
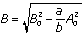 . By using this equation, we can determine the expected number of ships remaining in the winning fleet at the end of the battle. For example, two equal forces (
. By using this equation, we can determine the expected number of ships remaining in the winning fleet at the end of the battle. For example, two equal forces (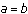 ) with
) with 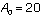 and
and 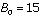 would result in a victory for A with 13 ships remaining after the battle. This surprisingly large number is a result of the two exponential functions above. The total number is decreasing exponentially, but the difference in the size of the fleets is increasing exponentially.
would result in a victory for A with 13 ships remaining after the battle. This surprisingly large number is a result of the two exponential functions above. The total number is decreasing exponentially, but the difference in the size of the fleets is increasing exponentially. -
If Nelson's 27 ships fought a conventional battle against the 34 ships in the French/Spanish Armada with
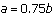 , then
, then 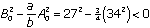 , and Nelson would lose. The expected number of ships remaining in the winning French/Spanish fleet would be
, and Nelson would lose. The expected number of ships remaining in the winning French/Spanish fleet would be  or 14 ships. (We will consider a "fractional ship" as still capable of fighting if the fraction is greater than one-half.) This would not be a good day for Admiral Nelson and the British.
or 14 ships. (We will consider a "fractional ship" as still capable of fighting if the fraction is greater than one-half.) This would not be a good day for Admiral Nelson and the British. -
First Battle (Fleet A, the French/Spanish Armada, Wins) Second Battle (Fleet B, the British, Wins) Final Battle Winner British French/
SpanishSurvive British French/
SpanishSurvive British French/
SpanishSurvive 4 17 16 23 17 18 18 16 11 British 5 17 16 22 17 16 16 16 8 British 6 17 16 21 17 15 15 16 6 British 7 17 15 20 17 14 14 15 5 British 8 17 14 19 17 12 12 14 2 French/
Spanish9 17 13 18 17 10 10 13 6 French/
SpanishThe number in the Survive column is the number of ships remaining after the battle. For example, looking at the first row, the British have 27 ships and the Armada has 34. The British split the battle into a fight of 4 British ships against 17 Armada. They lose, with the Armada having 16 ships left. The remainder of the British fleet (23 ships) fights a battle against the remaining 17 in the Armada. The British win with 18 ships surviving. Those 18 winning British ships from the second battle fight the 16 winning Armada ships from the first battle. The British win with 11 ships remaining at the end.
The table shows that Nelson has many options. However, he will want the first battle (the one he loses) to last as long as possible, so that the second battle will have the best chance of concluding before the survivors of the first battle can rejoin the fight. Having 7 ships in the first battle and 20 in the second allows Nelson to defeat the larger fleet with an expected 5 ships surviving.
The actual battle had more ships and did not follow this outline, but Nelson's original, creative strategy changed naval history.
References
Bartkovich, Kevin, et al. Contemporary Calculus Through Applications. Providence, Rhode Island: Janson Publications, 1995.
Bonder, Seth. "Mathematical Modeling of Military Conflict Situations." In Proceedings of Symposia in Applied Mathematics, edited by Saul Gass. Vol. 25, Operations Research Mathematics and Models. Providence, Rhode Island: American Mathematical Society, 1981.
Coleman, Courtney S. "Combat Models." In Modules in Applied Mathematics, edited by William Lucas. Vol. 1, Differential Equation Models, edited by Martin Braun, Courtney Coleman, and Donald Drew. New York: Springer-Verlag, 1983.
Authored by
Dan Teague
The North Carolina School of Science and Mathematics
Durham, North Carolina