AP Physics Featured Question: Raft with Hanging Weights
Question and Solution
An unoccupied, 10 kg wooden raft made of driftwood with specific gravity 0.60 floats on the surface of a calm pond. [The density of water is 1,000 kg/m3.]
-
What is the volume of the raft?
Since density is mass / volume, the volume of the raft is its mass divided by its density. Specific gravity of 0.60 by definition means 0.60 times as dense as water, so the raft's density is 600 kg/m3. The raft's volume calculates to be (10 kg) / (600 kg/m3) = 0.017 m3. [This is equivalent to 17 L, or to 17,000 cm3.]
-
Determine the buoyant force acting on the raft while it floats.
The raft is in equilibrium. The only downward force on the raft is: mg = 100 N. The only upward force is the buoyant force, so that force must also be equal to 100 N.
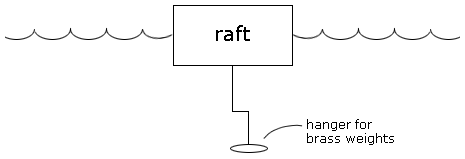
Now a student hangs brass (density = 8,000 kg/m3) masses under the water on a light string attached to the raft, as shown in the diagram above. The student adds brass a little at a time until the moment when the raft becomes completely submerged.
-
Determine the new buoyant force on the raft.
By Archimedes' principle, the buoyant force on the raft is equal to the weight of the water displaced. Since the raft is completely submerged, a volume of 0.017 m3 of water was displaced. The density of water is 1,000 kg/m3. The mass of water displaced is (1,000 kg/m3)(0.017 m3) = 17 kg, which weighs 170 N. So the buoyant force on the raft is 170 N.
-
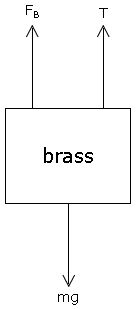
Calculate the minimum mass of brass that the student must hang from the raft to allow the raft to become completely submerged.

-
Start with an equilibrium equation for the raft:
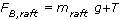
-
From previous parts of the question, we know
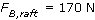 and
and 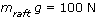 . The tension is found to be 70 N. Now write an equilibrium equation for the brass, noting that the tension in the rope will be 70 N:
. The tension is found to be 70 N. Now write an equilibrium equation for the brass, noting that the tension in the rope will be 70 N:
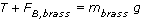
-
Now replace
 with
with 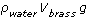 and
and 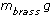 with
with 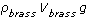 . We can solve for the volume of the brass:
. We can solve for the volume of the brass:
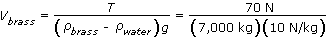
-
This gives a volume for the brass of 0.0010 m3. The mass of the brass is its density times its volume:
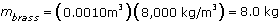
-
If instead the 10 kg raft were made of freshly cut wood with specific gravity 0.80, how would the answer to part (d) change? Choose one answer and justify it briefly.
 More brass would be necessary.
More brass would be necessary.
X Less brass would be necessary.
 The same amount of brass would be necessary.
The same amount of brass would be necessary.Look at the free-body diagram for the raft. With a higher density of wood but the same mass of wood, the volume of water that the wood displaces is smaller. So the buoyant force on the raft is less than 170 N. To maintain equilibrium, less than 70 N of downward tension is necessary. Thus less brass than before should be used.
Commentary
- The most common mistake is neglecting to include the buoyant force on the brass weights. This makes the question far, far simpler; the answer would be just to add 7.0 kg (70 N) of brass. The good news is that if this were scored like an AP question, a solution without the buoyant force on the brass would still earn probably 10 or 11 out of 15 points.
- It's interesting to note that because the brass experiences a buoyant force, its effective weight under water is less than its weight in air. That's why we have to add more brass than just 70 N; 80 N of brass has an effective weight under water of 70 N.
- When dealing with static fluids, I repeatedly emphasize getting comfortable relating mass, volume, and density correctly. Using long subscripts (as in the solution above) is a useful method of keeping track of which density, mass, or volume is referenced. For example, in this question, when students write the equation for the buoyant force on the brass, they shouldn't just write
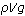 ; rather, they should write
; rather, they should write 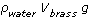 . That notation makes it easy to differentiate the buoyant force from the weight of the brass, which is
. That notation makes it easy to differentiate the buoyant force from the weight of the brass, which is 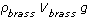 .
. - In a timed test situation, many students will struggle with part (d). It is important, though, that they take the time to approach the conceptual question in part (e) even if they can't get part (d)! Part (d) will appeal to the quantitative problem solvers in the class, but part (e) can be answered correctly by students with strong physical insight, no matter how poor their algebra skills. This is a good question on which to emphasize a smart approach to managing the AP Exam: look at every part of every problem, because you might be able to get full credit on subsequent parts even after struggling with a previous part.
Follow-Up Ideas
- Demonstration: Hang a metal mass by a string from a spring scale (or from a force probe). When the mass is submerged in water, the reading in the scale will drop. Students can see why the 8 kg of submerged brass will provide only 70 N of tension in the rope attached to the raft.
- The above demonstration can be made quantitative. Use a graduated cylinder to measure the volume of the metal mass. The buoyant force on the submerged mass will be equal to the weight of an equal volume of water. If the weight has a volume of, say, 25 mL, then the buoyant force it experiences will be 0.25 N: the reading on the spring scale should drop by a quarter of a newton.
- If the question was assigned for homework, part (e) of the AP-style question can be used as a comprehension quiz. Allow students to use their notes and their own solution to the homework question to answer the conceptual question posed in part (e).
- Laboratory exercise: Float a Styrofoam cup on the surface of a beaker filled to the brim with water. Add a measured amount of mass to the floating cup; collect the water that overflows. Graph the weight of the collected water versus the weight of the mass in the cup. Such a graph should form a line of slope 1. (Be careful about units: weights for the water and the masses must be measured in identical units for the slope to be 1.)
Follow-Up Quiz
(Bold type indicates changes from the questions asked in the original, AP-style question.)
An unoccupied, 10 kg wooden raft made of driftwood with specific gravity 0.80 floats on the surface of a calm pond. [The density of water is 1,000 kg/m3.]
-
Determine the buoyant force acting on the raft while it floats.
Answer: 100 N
Now a student hangs brass (density = 8,000 kg/m3) masses under the water on a light string attached to the raft. The student adds brass, a little at a time, until the moment when the raft becomes completely submerged.
-
Determine the new buoyant force on the raft.
Answer: 130 N
-
Calculate the minimum volume of brass that the student must hang from the raft to allow the raft to become completely submerged.
Answer: 4.3 x 10-4 m3, which would give a mass of 3.4 kg
-
Imagine that the student hangs slightly more than the minimum amount of brass from the raft. Describe the subsequent motion of the raft.
Answer: The raft will speed up toward the bottom of the tank because there will be a nonzero downward acceleration.
Authored by
Greg Jacobs
Woodberry Forest School
Woodberry, Virginia