AP Physics 2 Featured Question: Charged Particle in a Magnetic Field
Question
Consider a charged particle moving through a magnetic field that is not necessarily uniform. The particle follows a path that is not always parallel to the magnetic field’s direction. The magnetic force is the only force that acts on the particle.
(a) For this part, assume that the particle does not lose energy to electromagnetic effects due to the effects of acceleration and that the charge moves with a non-relativistic initial speed.
- The particle’s direction of motion will change but not its speed. This occurs regardless of its own charge or motion or the magnetic field’s strength or orientation. Briefly explain why this is.
- If the magnetic field is uniform in both strength and direction and the particle’s initial motion is perpendicular to the magnetic field direction, the particle will travel in a circular path. Explain why this occurs.
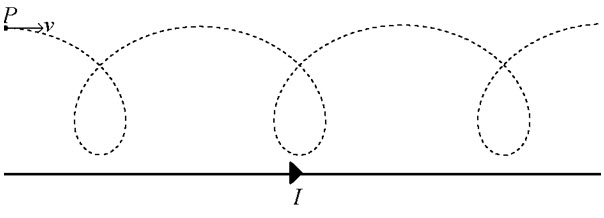
(b) The particle is initially located at point P in the plane of the page and moving to the right with speed v. The magnetic field that the particle moves through is generated by a long, straight wire carrying a current I to the right, located in the plane of the page below point P.
- Is the sign of the charge positive or negative? Explain how you arrived at your answer.
- The particle moves along the dotted path, which is entirely within the plane of the page (i.e. the dotted path is not a helix). This is due to the fact that the magnetic field generated by a long, straight, current-carrying wire is not uniform in strength. In a clear, coherent, paragraph-length response which may include equations and/or additional figures, explain why the particle’s path appears as it does above rather than being circular. Be sure to address specific features of the magnetic field’s strength and how that field strength affects the motion of the charge.
Solution
(a-i) 2 points
- The student shows understanding that the magnetic force on the particle is at all times perpendicular to the direction of the particle’s velocity.
- The student shows understanding that a net force that acts perpendicular to an object’s velocity cannot change the object’s speed. The student may use work and energy principles to make this argument but this is not necessary.
Example:
A magnetic field can only exert force on the charge perpendicular to the charge’s velocity vector. But force must be acute with velocity to speed an object up or obtuse to slow an object down. Since the force is perpendicular to velocity, the charge can’t change speed.
Example:
Magnetic force is always perpendicular to velocity. If a force is perpendicular to an object’s motion, no work is done by that force. Therefore, the magnetic force cannot change give or take kinetic energy from the object so the object cannot speed up or slow down.
Alternate Solution
- The student makes a general declaration that magnetic fields cannot perform work on an object.
- The student recognizes that net work on an object changes the object’s kinetic energy, so no net work means no change in the particle’s kinetic energy or speed.
Example:
Magnetic fields never do work. Since work causes an object’s kinetic energy to change, no net work means no change in speed.
(a-ii) 1 point
- The student shows understanding that the radius-of-curvature of an object’s path depends on the strength of the centripetal force, and states that a uniform magnetic field produces a constant force on the particle.
(b-i) 2 points
The particle has a positive charge. This conclusion must be reached to earn both points.
- The student chooses a location on the particle’s dotted path, and correctly indicates the direction of velocity and magnetic force at that point. (If a “high point” on the dotted line is chosen, such as P, the velocity is to the right and the force is down, “toward the center” of the curvature. If a “low point” closest to the wire is chosen on the dotted line, the velocity is to the left and the force is up.)
- The student recognizes that the wire’s magnetic field is directed out of the page in the region where the particle is moving.
If either of these ideas is stated, one point is earned. Both points are only earned if the student connects their velocity, magnetic field, and net force directions to the correct charge sign.
(b-ii) 5 points
- The student recognizes that the radius of curvature of the particle’s path decreases as the particle moves closer to the wire.
- The student explains that the magnetic field strength is stronger closer to the wire. The student may use the equation
 as part of their explanation of this idea.
as part of their explanation of this idea. - The student explains that the stronger the magnetic field, the stronger the magnetic force acting on the particle. The student may use the equation
 as part of their explanation of this idea.
as part of their explanation of this idea. - The student states or implies that the magnetic force provides the centripetal force for the particle. The student furthermore explains that a stronger centripetal force results in a shorter radius of curvature for an object. The student may use the equation
 as part of their explanation of this idea.
as part of their explanation of this idea. - For a logical, relevant, and internally consistent response that addresses the require argument or question asked, and follows the guidelines described in the published requirements for the paragraph-length response.
Example:
The path at point P is very straight, but close to the wire the path is sharply curved. This is because the magnetic field close to the wire is stronger, exerting more force on the charge. Because magnetic field is always perpendicular to speed, the magnetic force can only “steer” the charge’s direction. A stronger force is like turning the steering wheel harder on a car—it makes the path sharper and have lower radius. This is what occurs close to the wire where the magnetic field is strong, but far from the wire where the field is weak, the charge doesn’t change direction as quickly and the path has a larger radius.
Commentary
This problem was inspired by Free Response #5 on the released free response questions for the 2016 AP Physics 1 exam (P1-2016-FR05 for short). On that problem, a vertical string holds a standing wave that has different wavelengths in different places due to the differing tensions in the string. We often teach standing waves in media where the wave speed is the same throughout; this results in standing wave patterns having the same-sized node-antinode distance. In the same way, we often teach the motion of a charge through a magnetic field only in the special case where the magnetic field is uniform. This problem tests whether students understand qualitatively how magnetic field's affect the radius-of-curvature of a charged particle's path even as the magnetic field varies from place to place.
The problem begins with a statement that magnetic force cannot change the speed of a charge. The problem does this so that students can use this fact later as part of their paragraph-length response, even if they do not know why this is the case (much as part (a) of P1-2016-FR05 directly states that the tension is greater near the top of the rope and asks why, so that students who do not know why can still use this fact later in part (b)). The question about why a uniform field results in a circular path is set in place in order to prepare students to compare and contrast the uniform circular motion of a charge in a uniform B-field with the non-uniform, non-circular motion of a charge in a non-uniform B-field that occurs on part (b).
Then the question moves on to a charge in the vicinity of a long, straight wire. The first part of this challenge asks students to state the sign of the charge and explain how they arrived at their answer. Many teachers simply drill students on problems such as "here is the charge's sign, velocity direction, and the direction of the magnetic field that the charge is in; now tell me the direction of the magnetic force on the charge." While this is a valuable an unavoidable part of teaching magnetism, it is highly unlikely that students will see such a direct question about applying the right-hand-rule on a Physics 2 exam. Instead, students will need to consider a more complex situation and be able to take from the situation three of these things (charge sign, charge velocity direction, magnetic field direction, and direction of magnetic force) and determine the fourth.
The second part of the charge-and-wire is the reason why we have this problem: to determine whether the student can understand principles and relationships in the context of a topic that they have learned but a situation that they are unlikely to have encountered before. In this case, the student must combine the following ideas together to explain why the charge follows the dotted-line path:
- The path has small radius of curvature close to the wire and long radius of curvature far away. Students can be taught during AP Physics 1 to recognize long and short radius-of-curvature paths. This can be done in the context of roads and driving; draw a curve on the board and say that the curve represents a road as seen from above. Draw the curve so that there are clear places where the radius of curvature is large and where it is small and ask students to explain where cars can go faster or where they must go slower.
- The magnetic field is stronger at locations closer to the wire. This is usually taught as part of a typical magnetism unit using the equation for magnetic field due to a straight wire.
- A stronger magnetic field exerts a stronger force on a charge. This is taught as part of teaching the equation
 . Note that students need to know that only B can affect the value of F, since a magnetic field cannot change the speed v of a particle and the charge depends on the particle's properties.
. Note that students need to know that only B can affect the value of F, since a magnetic field cannot change the speed v of a particle and the charge depends on the particle's properties. - The magnetic force is perpendicular to the motion, so the magnetic force provides the centripetal force on the particle.
- The stronger the centripetal force on an object, the "tighter the turn" (smaller radius-of-curvature path) the particle can make. This again should be introduced in Physics 1, again in the context of roads with different radii-of-curvature at different places. Students should be able to understand that more force is required to make a tighter turn because the motion changes more rapidly in these cases.
Quiz
Four particles move in the vicinity of a long wire carrying current I. The particles have masses and charges as shown in the table. The wire and all particles are in the plane of the page as shown in the diagram. The arrow on each particle represents that particle’s initial motion. The grid can be used to quantify the locations and relative speeds of the particles. The only force that acts on each particle due to the wire’s magnetic field.

(a) Which two particles experience magnetic forces in the same direction at the instant shown in the diagram? Explain how you arrived at your answer.
(b) Rank the particles according to the magnitudes of the forces acting on that particle from strongest to weakest. Put the symbol > or = between each letter of your ranking.
Strongest Force ____ ____ _____ _____ Weakest Force
Justify your answer quantitatively, using equations.
(c) Rank the particles according to the magnitudes of each particle’s acceleration from greatest to least.
Justify your answer quantitatively, using equations.
Greatest Acceleration ____ ____ _____ _____ Least Acceleration
Each particle makes a circular motion in the wire’s magnetic field. All of the circular motions have radii that are very small compared to the particle’s distance from the wire, so that the magnetic field around each circle can be assumed to be uniform.
(d) Which particle or particles make a counterclockwise circular motion? Explain how you arrived at your answer.
(e) Rank the particles according to the radius of each particle’s circular motion from greatest to least.
Justify your answer quantitatively, using equations.
Greatest Radius ____ ____ _____ _____ Least Radius
(f) Rank the particles according to the period of each particle’s circular motion from longest to shortest.
Justify your answer quantitatively, using equations.
Longest Period ____ ____ _____ _____ Shortest Period
Solutions
17 total points.
(a)
- Above the wire, the magnetic field is out of the page. The magnetic field is into the page below the wire.
- Particle P feels leftward force (positive, moving down, out of the page magnetic field).
- Particle N feels upward force (negative, moving left, into the page magnetic field).
- Particle D feels downward force (positive, moving right, out of the page magnetic field).
- Particle A feels leftward force (positive, moving up, into the page magnetic field).
- (1 point) P and A feel the same magnetic force.
- (1 point) Citing a hand rule.
(b)
- (1 point) The correct ranking is N = D > A > P
- (1 point) Indicating that the magnetic field is proportional to 1/y, where y is the distance of the charge from the wire. Using the equation
 would satisfy this requirement.
would satisfy this requirement. - (1 point) Indicating that
 .
. - (1 point) Putting these equations together to find that force is proportional to
 . Stating the full equation
. Stating the full equation  satisfies the last three points.
satisfies the last three points.
(c)
- (1 point) The correct ranking is N > D > P > A
- (1 point) Stating and using Newton’s Second Law,
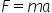 . Using
. Using 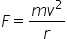 does NOT earn this point.
does NOT earn this point. - (1 point) Using the previous expression for force to find acceleration proportional to
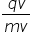 . Stating the full equation
. Stating the full equation 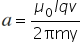 satisfies the last three points.
satisfies the last three points.
(d)
- (1 point) A is the only particle that moves counterclockwise.
- (1 point) The student indicates that the force direction must be 90o counterclockwise from the velocity direction for counterclockwise circular motion, or some other convincing argument.
(e)
- (1 point) The correct ranking is D = A > P = N
- (1 point) Setting the magnetic force equal to the centripetal force,
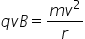 , or setting the acceleration found in (c) equal to
, or setting the acceleration found in (c) equal to 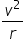 .
. - (1 point) Solving for radius to find
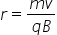 and finding that radius is proportional to
and finding that radius is proportional to 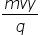 or coming up with a full equation for r that shows mvy in the numerator and q in the denominator.
or coming up with a full equation for r that shows mvy in the numerator and q in the denominator.
(f)
- (1 point) The correct ranking is A > P = D > N
- (1 point) Using the equation
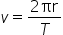 .
. - (1 point) Solving for period to that period is proportional to
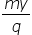 or some other equation that shows this relationship.
or some other equation that shows this relationship.
Author
John Frensley
Prosper High School
Prosper, Texas