An Energy Primer for the AP Environmental Science Student
Even for practicing scientists and engineers, energy concepts and terminology can sometimes be confusing and ambiguous. Confusion arises because different disciplines often employ different systems of measurement and use specialized vocabulary unique to a particular industry. The situation can be especially troublesome for the introductory environmental science student who may not have completed even a first course in physics. And the problem is not alleviated by the typical environmental textbook, in which energy terms are introduced only in a piecemeal fashion as needed in the context of a specific environmental topic. Thus, the introductory environmental science student is often left with a fragmentary, confusing, and unsatisfactory introduction to energy concepts and terminology. This is particularly worrisome because energy use is at the heart of most environmental problems. Moreover, the environmentalist must be able to communicate with people in many different disciplines. Accordingly, he or she must be familiar with the different systems of measurement and be able to convert readily from one to another. This article provides a brief introduction to the major systems of measurement used in science and technology with a special focus on energy terms useful for the environmentalist.
Systems of Measurement
There are two systems of measurement in common use in the world: the United States Customary System (USCS, formerly called the British system) of feet, pounds, and seconds, in everyday use in the United States, and the metric system of meters, kilograms, and seconds, in use everywhere else. In 1960 the metric system was adopted by an international committee in Paris as the worldwide standard for science and is now referred to as the Système International or SI. The U.S. is the only major country that still uses the British system of measurement (even Britain has gone metric!), but this system is well ingrained in American society and is unlikely to see an early demise. A subset of the metric system is the centimeter-gram-second (cgs) system that is commonly used in atomic physics and chemistry.
All physical quantities, such as velocity, acceleration, force, momentum, and energy, ultimately can be expressed in terms of three basic units of length, mass, and time. These three quantities are referred to as fundamental units because they can be used to define all other elements in a particular system of measurement. The table below summarizes the fundamental units for the three common systems of measurement.
| System | Length | Mass | Time |
|---|---|---|---|
| SI (mks) | meter | kilogram | second |
| SI (cgs) | centimeter | gram | second |
| USCS (fps) | foot | slug | second |
Because the mass unit slug is uncommon, the USCS is referred to as the foot-pound-second (fps) system, but strictly speaking, the pound (lb) is a unit of force, not mass. Conversely, in the SI system the mass unit of kilogram is often used to express force (of gravity), as in a person’s weight, for example. In this sense, a convenient conversion factor between the systems is to use the “weight equivalent” of 2.2 lbs for a 1 kg mass.
Work and Energy
Physicists define energy as “the ability to do work,” but in a sense this begs the question because work itself is still undetermined. The term “work” in physics is defined as force multiplied by the distance through which the force acts. Thus we get the idea that energy is the property that allows one to move objects from one place to another and thereby accomplish some physical labor or “work.” Energy itself may appear in a variety of forms — e.g., solar energy, electrical energy, chemical energy, thermal energy, and nuclear energy — but the bottom line is that all forms can be used to do work. Thus, all units of energy must ultimately be reducible to those of work — i.e., force x distance. From Newton’s law, we know that force is mass x acceleration. So extending the above table, we have:
| System | Force = | Mass x | Acceleration |
|---|---|---|---|
| SI (mks) | newton | kg | m/s2 |
| SI (cgs) | dyne | gram | cm/s2 |
| USCS (fps) | lb | slug | ft/s2 |
And finally, we have the table for energy:
| System | Energy = | Force x | Distance |
|---|---|---|---|
| SI (mks) | joule | newton | meter |
| SI (cgs) | erg | dyne | cm |
| USCS (fps) | ft-lb | lb | ft |
Note that although the newton and joule are named for persons, they are not capitalized when used as a unit of measurement. However, the corresponding symbols (N and J) are capitalized when used independently.
The Newton
The SI unit of force, the newton (N), is of course named in honor of Isaac Newton. From the above, we see that 1 N = 1 kg-m/s2, which is equivalent to about 0.225 lbs. Note that 1 N is not equal to the weight of 1 kg.
The Joule
Similar to the unit of force, the joule (J) is named in honor of Sir James Prescott Joule, a famous 19th-century British scientist who performed many precise energy experiments. One joule is the amount of work done by a force of one newton acting through a distance of one meter. From a practical, everyday standpoint, the joule is a relatively small amount of energy, but it is used most often in scientific work. The energy content of one large donut, for instance, is about 106 joules.
The Calorie
Through a series of cleverly designed experiments with pulleys, weights, paddle wheels, and precisely measured temperatures in containers of water, Joule convincingly demonstrated the equivalence between mechanical energy and heat. Until that time, people thought that heat was some sort of ephemeral property of materials, like a fluid, that was released when solid objects were broken into smaller pieces. They called this property caloric, from which the term calorie is derived. Joule showed that heat and mechanical energy are equivalent, and his careful measurements gave us what we refer to today as the “mechanical equivalent of heat”:
1 calorie = 4.186 joules.
You may recall that one calorie is the amount of heat required to raise the temperature of one gram of water by one Celsius degree. One kilocalorie would increase the temperature of 1 kg of water by the same amount. The kilocalorie is sometimes referred to as a “big” calorie and written with a capital C, namely, as Calorie. Obviously, this practice has much potential for confusion, so the reader must be constantly alert as to a writer’s intention when speaking of calories. To further confuse the issue, food calories are always “big” calories. Thus, when one speaks of 100 Calories in a slice of bread, for instance, the implication is that 100 kilocalories or 4.186 x 105 J would be released through burning the dried biomass.
The energy content in fuels is measured by burning them to exhaustion and capturing the heat that is released. This heat can be transferred, say, to a container of water where a temperature increase is measured. Knowing that one calorie per gram is required to increase the temperature of the water then allows one to determine the energy content of the fuel in terms of calories. This number can then be converted to other energy units using Joule’s conversion factor.
The Btu
Another popular unit of heat energy is the Btu (British thermal unit). One Btu is the amount of heat required to raise the temperature of one pound of water by one degree Fahrenheit. Using the conversion factors of 2.2 lbs/kg and 1.8 F°/C°, and Joule’s equivalent, we find that:
1 Btu = 252 cal = 1055 J.
One Btu is approximately the amount of heat released by burning one large kitchen match.
Btus are commonly used in the United States to rate water heaters, furnaces, and air conditioners. A typical natural gas household water heater, for instance, might be rated at 40,000 Btu/h and a furnace at twice this, or 80,000 Btu/h. These numbers, of course, give the rate at which heat can be produced by the burners of these units. The heating values for fuels are often stated in terms of Btus per unit weight. Coal, for instance, has a typical heating value of 25 million Btu/ton, and petroleum 37 million Btu/ton.
The Therm
Gas companies in the U.S. often measure sales in terms of “thermal units” or therms. One therm is defined as 100,000 Btu, and natural gas at normal temperature and pressure has a heat value of 1,030 Btu/ft3. Thus, one therm is very nearly equal to 100 cubic feet of natural gas:
1 therm = 105 Btu / 1,030 Btu/ft3 = 97.1 ft3 ≈ 100 ft3.
Gas companies also use “American Engineering” terminology instead of standard SI scientific notation. In this notation, the Latin abbreviations of C for 100 and M for 1000 are employed as numerical prefixes, but because of the potential confusion between the standard scientific notation of C for centi (10-2) and M for mega (106), the engineering abbreviations are not usually written with capitalization. For instance, 1 ccf = 100 cubic feet, and 1 mcf = 1,000 cubic feet, and one million cubic feet is written as 1,000 x 1,000 cf or 1 mmcf.
Power
Power is the term that is used to describe energy flow. Power is defined as “the time rate of doing work” and normally is measured in joules/second. In the SI system, the unit of power is the watt (W), named in honor of James Watt, inventor of the steam engine.
1 watt = 1 joule/second.
No separate unit is ascribed to power in the cgs system. In the USCS system, power is measured in “practical” units of horsepower (hp), where 1 hp = 550 ft-lbs/s. This is equivalent to 746 watts, or about 0.75 kW.
Perhaps because most electric appliances are rated in terms of their power requirements, power and energy are often confused when dealing with electrical energy. But just as when filling the tank of your car at the gas station you must ultimately pay for the total number of gallons pumped, not the rate at which you pumped it, so with electricity we pay for the total number of joules of electrical energy consumed, not the power or rate at which it was delivered.
In the U.S., electrical energy is usually measured in terms of kilowatt-hours (kWh), because this is a practical unit for the utility company as well as the customer. The relation between kilowatt-hours and joules is easy to determine:
1 kWh = 1,000 J/s x 3,600 s = 3.6 x 106 J.
Again, we see how small a joule is in practical terms. One kWh is the energy required to power ten 100-watt lightbulbs for one hour. The average home in the U.S. uses about 10,000 kWh of electrical energy per year.
Electric Power Plants
Electric utility power plants are rated in terms of their capacity to deliver electric power. For instance, a large coal-fired or nuclear plant might be rated at 1,000 MWe (megawatts). The “e” subscript on the W stands for “electric” and is a signal that the rating is for the “output” capacity of the plant, not the energy input. Input energy is usually measured in terms of the heating value for the fuel — Btus for coal, for instance. If the plant operates at, say, 40 percent efficiency, then the energy input required for such a plant can be computed as follows:
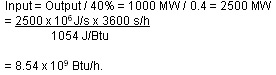 Input = Output/40% = 1000 MW/0.4 = 2500 MW = 2500 x 10⁶ J/s x 3600 s/h / 1054 J/Btu = 8.54 x 10⁹ Btu/h
Input = Output/40% = 1000 MW/0.4 = 2500 MW = 2500 x 10⁶ J/s x 3600 s/h / 1054 J/Btu = 8.54 x 10⁹ Btu/h
If this energy is supplied by coal with a heating value of 25 x 106 Btu/ton, then coal would need to be input at a rate of:
 8.54 x 10⁹ Btu/h / 25 x 10⁶ Btu/ton = 342 tons/hour.
8.54 x 10⁹ Btu/h / 25 x 10⁶ Btu/ton = 342 tons/hour.
Operating at full capacity 24 hours a day, such a plant would consume about three million tons of coal per year.
Solar Energy
Another valuable use of power in environmental analyses deals with solar energy. The sun, of course, provides radiant energy for all life on earth, and the rate at which this energy is received is referred to as solar flux, representing the power per unit area received at a given location. At the position of the Earth’s orbit, this number is about 1,400 W/m2 and is referred to as the solar constant. This means that a flat panel of 1 m2 placed outside the Earth’s atmosphere and oriented perpendicular to the sun’s rays would receive 1,400 joules per second of solar energy.
The atmosphere absorbs about half of this energy, so that 700 W/m2 is about the maximum amount that reaches the Earth on a hot summer day in the tropics. Averaging over day and night for all seasons and all latitudes, this is further reduced to about 240 W/m2 as the average solar radiation received at the Earth’s surface. Cloud cover and other factors reduce these numbers even further. In the U.S., for example, Tucson, Arizona, enjoys an annual average solar flux of 250 W/m2, but Cleveland receives only 160 W/m2. Obviously, such numbers have implications for the merits of solar heating and cooling as well as biomass growth in various locales.
Summary
Because energy plays a fundamental role in all environmental problems, it behooves the student to become familiar at an early stage with energy concepts and terminology. The environmental scientist must also get accustomed to specialized terms that are used in different disciplines and industries. The gas company is not going to convert cubic feet into Btus for you, just as the electric company is not going to convert kWh to joules. It is the responsibility of the environmental student to be able to put units on a common basis in order to make valid comparisons. For instance, is a natural gas furnace more economical or more environmentally benign than baseboard electric heating for an average home? Could solar energy supply all the heating needs for a home in Cleveland? How much electricity could be generated by installing solar panels on the roof of a home in Arizona? How much biomass can be grown on an acre of land in Missouri? A thorough understanding of energy units and terminology will go a long way toward helping the environmentalist make such analyses easy and commonplace.
Practice Questions
1. Given that 1 kcal of heat is required to increase the temperature of 1 kg of water by 1°C:
- How many kcals would be required to heat 100 kg of water by 20°C for a bath?
- How many joules is this?
- How many Btus?
- If your water heater can supply 40 kBtu/h, how long will it take to heat this water?
2.
- Given that 1 kWh = 3.6 MJ and that 1 Btu = 1055 J, show that 1 kWh = 3412 Btu.
- Why would it be incorrect to use this conversion factor directly to determine the amount of coal required to generate electricity in a power plant?
3. A typical home in the northern U.S. might require 120 MBtu of heat for the average winter.
- If this heat were supplied by a natural gas furnace operating at 60 percent efficiency, how many cubic feet of gas would need to be purchased?
- At a cost of $0.90/ccf, what would it cost to heat this house for one season?
- If a new 80 percent efficient furnace could be installed at a cost of $4,000, how long would it take to pay back the cost of this furnace assuming gas prices remained the same?
4. Suppose the house in question 3 is located in Cleveland where the annual average solar flux is 160 W/m2 2. If 10 m2 of solar panels operating at 20 percent efficiency were installed on this house to collect and store solar energy in the form of hot water:
- How much energy could be gained in one year in this manner?
- What fraction of the annual heating requirement is this?
- Using the hot-water heating requirements for a bath from question 1(c), how many hot baths would this energy supply in one year?
5. The annual average solar flux in Tucson is 250 W/m2. Suppose 10 m2 of solar electric panels operating at 10 percent efficiency were installed on a home there.
- How many kWh of electricity could be collected by these panels in one year?
- What fraction of the annual electrical requirement of 10,000 kWh for the average home does this represent?
- How many square meters of solar panels would be required to supply 10,000 kWh per year?
6. Solar energy is converted naturally into wood biomass with an efficiency of about 0.1 percent. Suppose a wood lot of 100 hectares (106 m2) is located in Missouri, where the average annual solar flux is 200 watts/m2. Given that the heat value for wood is 12 MBtu/ton, how many tons of wood can be produced by this property each year?
7. With moderate winds, a modern large wind turbine can generate about 250 kW of electricity, whereas a large nuclear power plant can generate 1,000 MW.
- How many wind turbines would be required to give the same output as one nuclear power plant?
- Discuss some of the advantages and disadvantages to providing electrical power by each method.
8. Batteries are usually rated in terms of ampere-hours, indicating the current that the cell is capable of delivering for a specified time. A typical D-cell flashlight battery, for instance, might be rated at 3 ampere-hours. The total electrical energy available from such a battery is found by multiplying the ampere-hour rating by the battery voltage. Thus this same 1.5 volt D cell could deliver 4.5 watt-hours of electrical energy.
Convert this energy to kWh and compare the cost of electrical energy derived in this manner to that of standard “grid-based” electricity. Assume that the battery costs $1.00 and that electricity from the power company is available at $0.10/kWh.
9. The table below gives prices and heat energy content for various fuels that are commonly used for home heating. Fuel prices are given as a per-unit cost for fuel delivered to the home. Complete the table by filling in the last two columns and thereby compare the cost of home heating by these various methods. In your computations, assume that the home requires 120 MBtu of heat for a season and that gas- or oil-fired furnaces operate at 80 percent efficiency. Assume that electrical heating is 100 percent efficient.
| Fuel | Price | Energy Content of Fuel | Cost per MBtu | Cost of Home Heating |
|---|---|---|---|---|
| Nat. gas | $1.14/ccf | 1030 Btu/cf | ||
| Propane | $1.69/gal | 92 k Btu/gal | ||
| Fuel oil | $1.93/gal | 133 k Btu/gal | ||
| Electricity | $0.10/kWh | 3412 Btu/kWh |
Answers
1. a. 2,000 kcal; b. 8.37 x 106 J = 8.37 MJ; c. 7,940 Btu; d. 11.9 minutes.
2. b. The second law of thermodynamics prevents 100 percent conversion of heat to mechanical or electrical energy. A typical coal-fired power plant operates at about 33 percent efficiency, meaning that only one-third of the energy in the coal is converted to electricity.
3. a. 1,941 ccf; b. $1,748; c. 9.2 years
4. a. 9.57 MBtu; b. 8 percent; c. 1,200
5. a. 2,190 kWh; b. 21.9 percent; c. 45.7 m2
6. 498 tons
7. a. 4,000; b. Answers vary
8. Battery energy: 4.5 Wh = 4.5 x 103 kWh.
Cost per kWh: $1.00 / 4.5 x 103 kWh = $222/kWh.
Comparison: Electrical energy from the battery costs $222 / $0.10 = 2,220 times as much as that delivered by the power company.
9.
| Fuel | Price1 | Energy Content of Fuel | Cost per MBtu | Cost of Home Heating1 |
|---|---|---|---|---|
| Nat. gas | $1.14/ccf | 1,030 Btu/cf | $11.07 | $1,660 |
| Propane | $1.69/gal | 92 kBtu/gal | $18.37 | $2,755 |
| Fuel oil | $1.93/gal | 133 k Btu/gal | $14.51 | $2,177 |
| Electricity | $0.10/kWh | 3,412 Btu/kWh | $29.31 | $3,5173 |
Notes
1. Prices quoted are for home delivery of respective fuels at rates available in the north central U.S. in 2005.
2. Computations assume a heating requirement of 120 MBtu for the “average” home in the northern U.S. Efficiencies of 80 percent are assumed for gas or oil furnaces. Heat from electricity is assumed to be delivered at 100 percent efficiency in the home.
3. Homes designed for electric heating are usually insulated more thoroughly than those designed for gas or oil.
Authored by
Thomas B. Cobb
Bowling Green State University
Bowling Green, Ohio